10: data visualization

STA35B: Statistical Data Science 2

Akira Horiguchi

Table of contents

• ggplot2
• Exploring the diamonds data set
• Communicating ideas

Purpose of visualizing data

1. Exploratory data analysis
2. Presenting findings to others

Affects how much effort to put in

• If just exploring data, a plot doesn’t need to look pretty if you can interpret it
• If high-stakes presentation (e.g. for job interview, raise, promotion, etc), might need to add many bespoke features (not focus of this class)

Exploratory data analysis

Cycle through the following:

• Generate questions about your data.

• Search for answers by visualizing, transforming, and modelling your data.

• Use what you learn to refine your questions and/or generate new questions

Requires creativity and critical thinking. Two question categories:

1. What type of variation occurs within each variable?
   • Mean, standard deviation, skewness, etc
2. What type of covariation occurs between variables?
   • How does height vary with weight, etc

ggplot2

Visualization

We’ll see how to create beautiful visualizations using ggplot2.

library(tidyverse)
library(palmerpenguins)
library(ggthemes) # color palettes for ggplot
penguins

# A tibble: 344 × 8
   species island    bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
   <fct>   <fct>              <dbl>         <dbl>             <int>       <int>
 1 Adelie  Torgersen           39.1          18.7               181        3750
 2 Adelie  Torgersen           39.5          17.4               186        3800
 3 Adelie  Torgersen           40.3          18                 195        3250
 4 Adelie  Torgersen           NA            NA                  NA          NA
 5 Adelie  Torgersen           36.7          19.3               193        3450
 6 Adelie  Torgersen           39.3          20.6               190        3650
 7 Adelie  Torgersen           38.9          17.8               181        3625
 8 Adelie  Torgersen           39.2          19.6               195        4675
 9 Adelie  Torgersen           34.1          18.1               193        3475
10 Adelie  Torgersen           42            20.2               190        4250
# ℹ 334 more rows
# ℹ 2 more variables: sex <fct>, year <int>

Basic structure of ggplot2

ggplot() constructs the initial plot.

• The first argument of ggplot() is the data set for the plot.
  • The data set must be a data frame.
• ggplot(data = mpg) creates an empty plot.

You then add one or more layers to ggplot() using +.

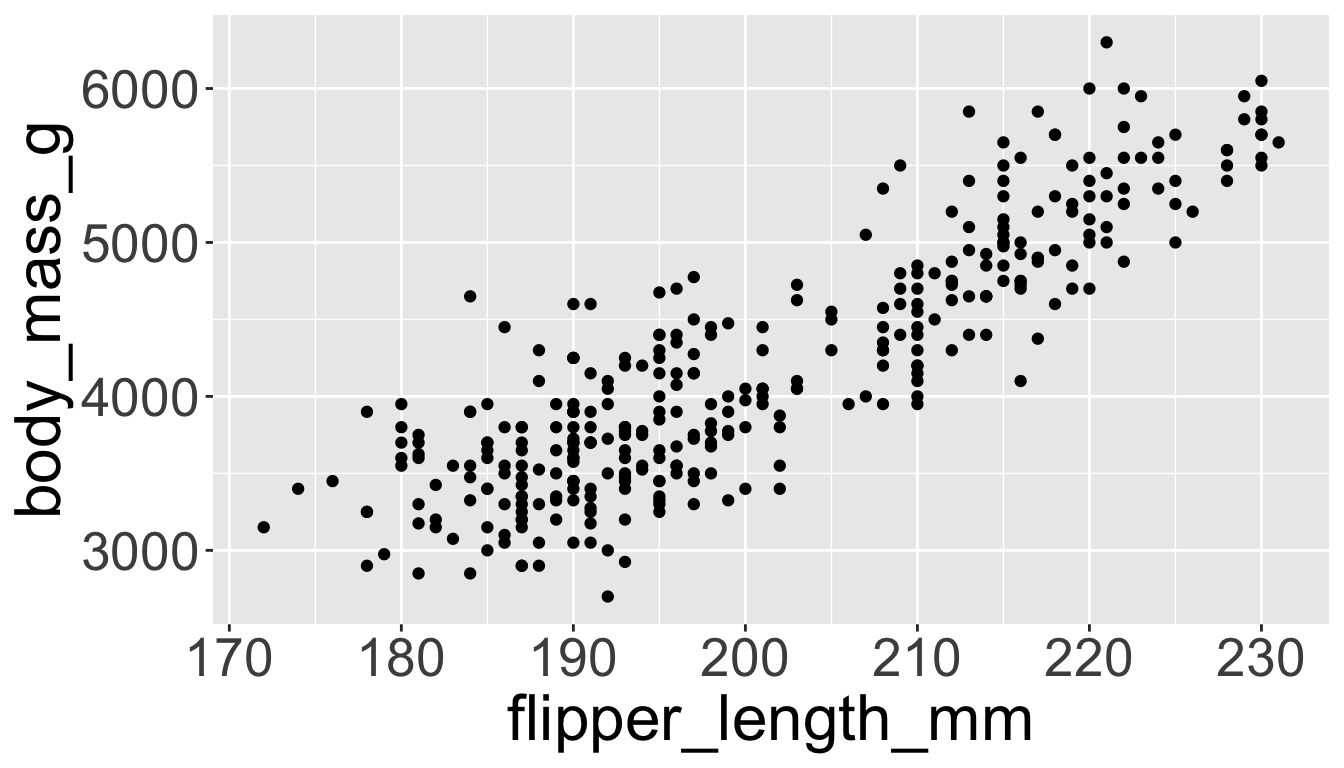
• geom functions add a geometrical object to the plot.
  • geom_point(), geom_smooth(), geom_histogram(), geom_boxplot(), etc.

Creating a ggplot

• Start with function ggplot()

penguins |> 
    ggplot()

Creating a ggplot

• Start with function ggplot()
• Add global aesthetics (i.e., aesthetics applied to every layer in plot).

penguins |> 
    ggplot(aes(x = flipper_length_mm, 
               y = body_mass_g)) 

Creating a ggplot

• Start with function ggplot()
• Add global aesthetics (i.e., aesthetics applied to every layer in plot).
• Add layers.
  • Display data using geom: geometrical object used to represent data
  • geom_bar(): bar chart; geom_line(): lines; geom_boxplot(): boxplot; geom_point(): scatterplot

penguins |> 
    ggplot(aes(x = flipper_length_mm, 
               y = body_mass_g)) +
    geom_point()

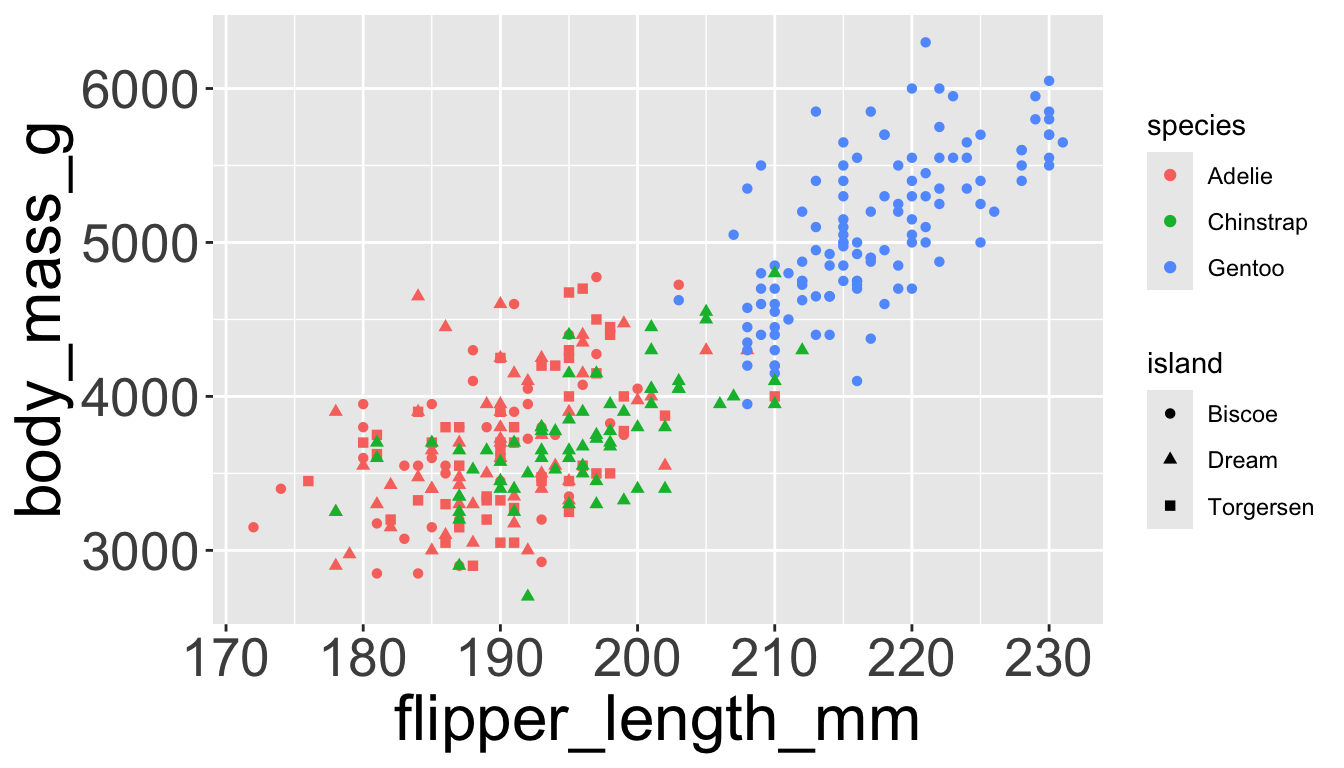
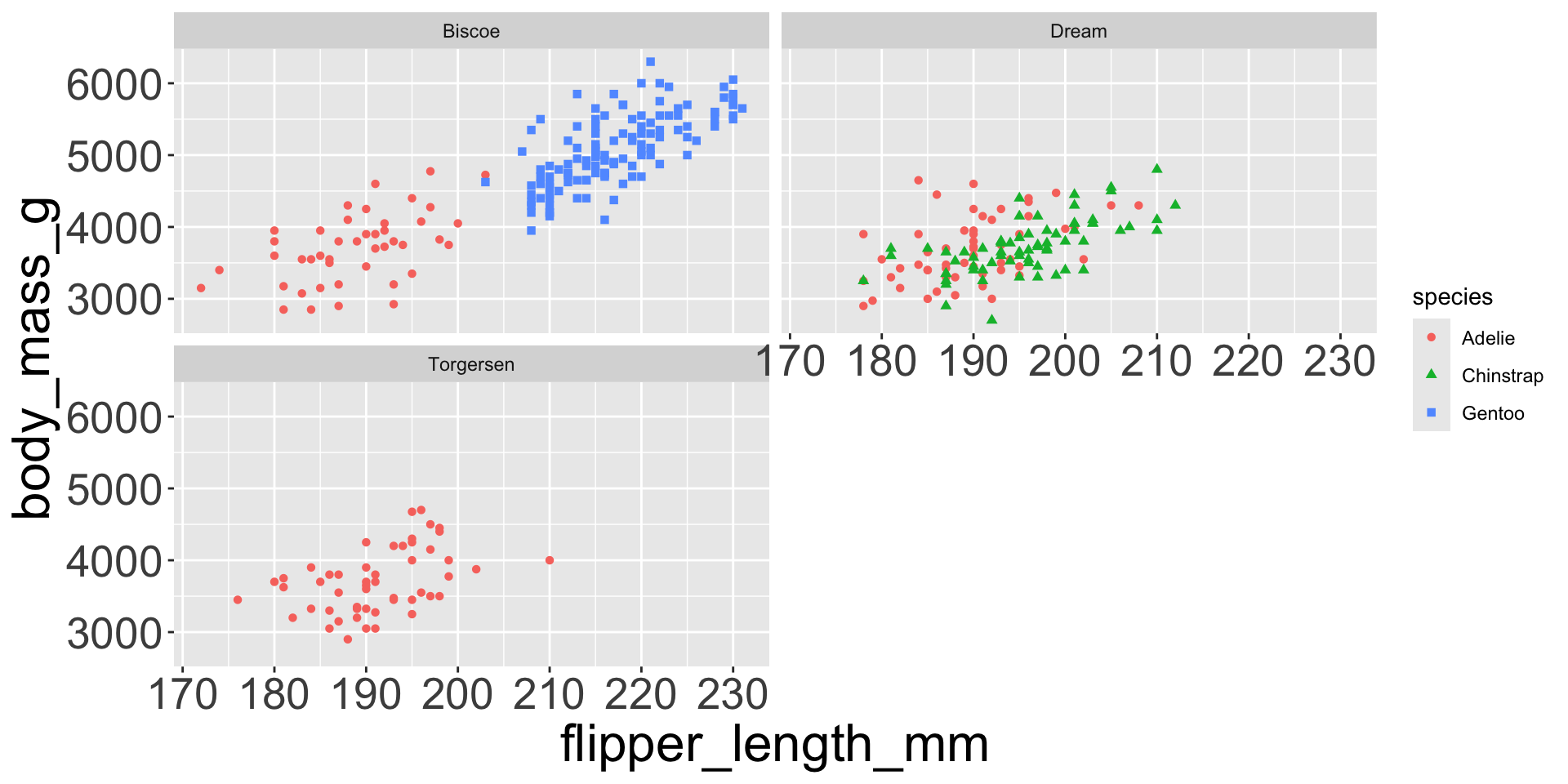
Adding aesthetics and layers

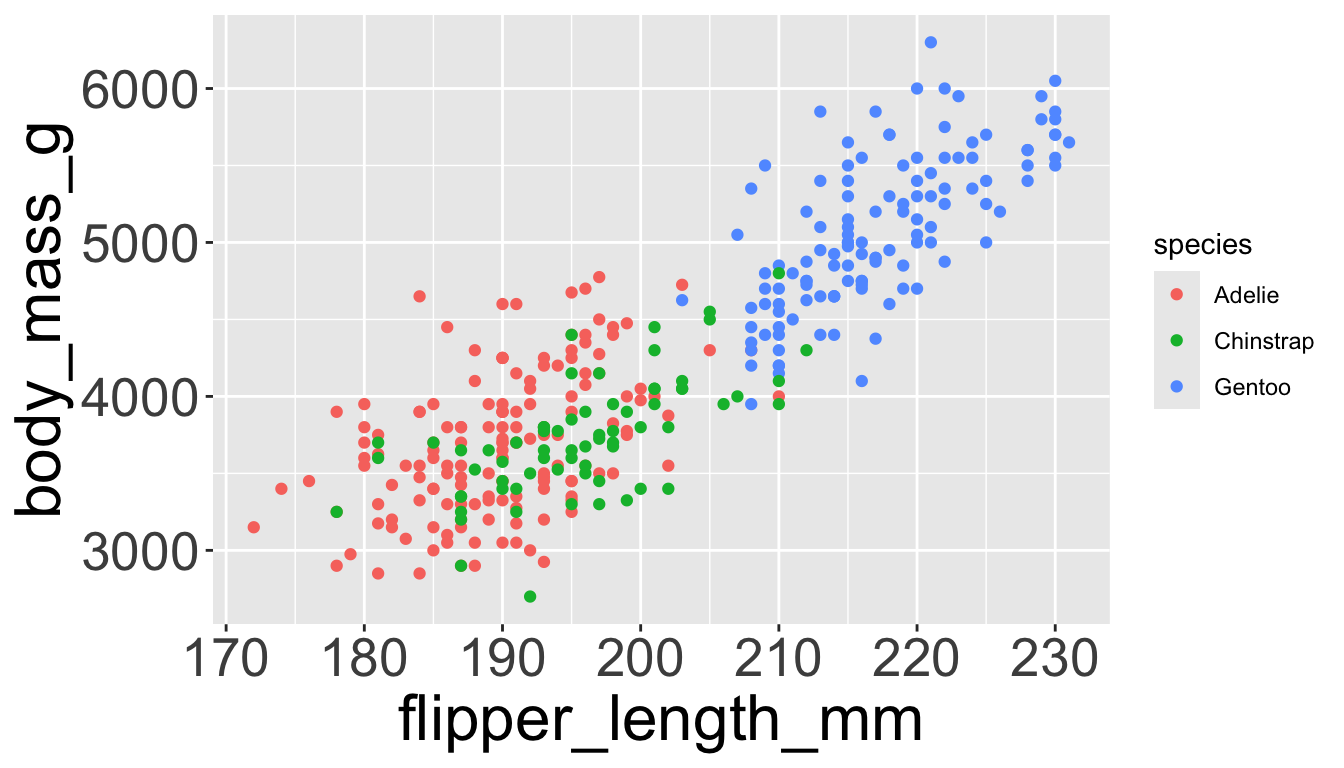
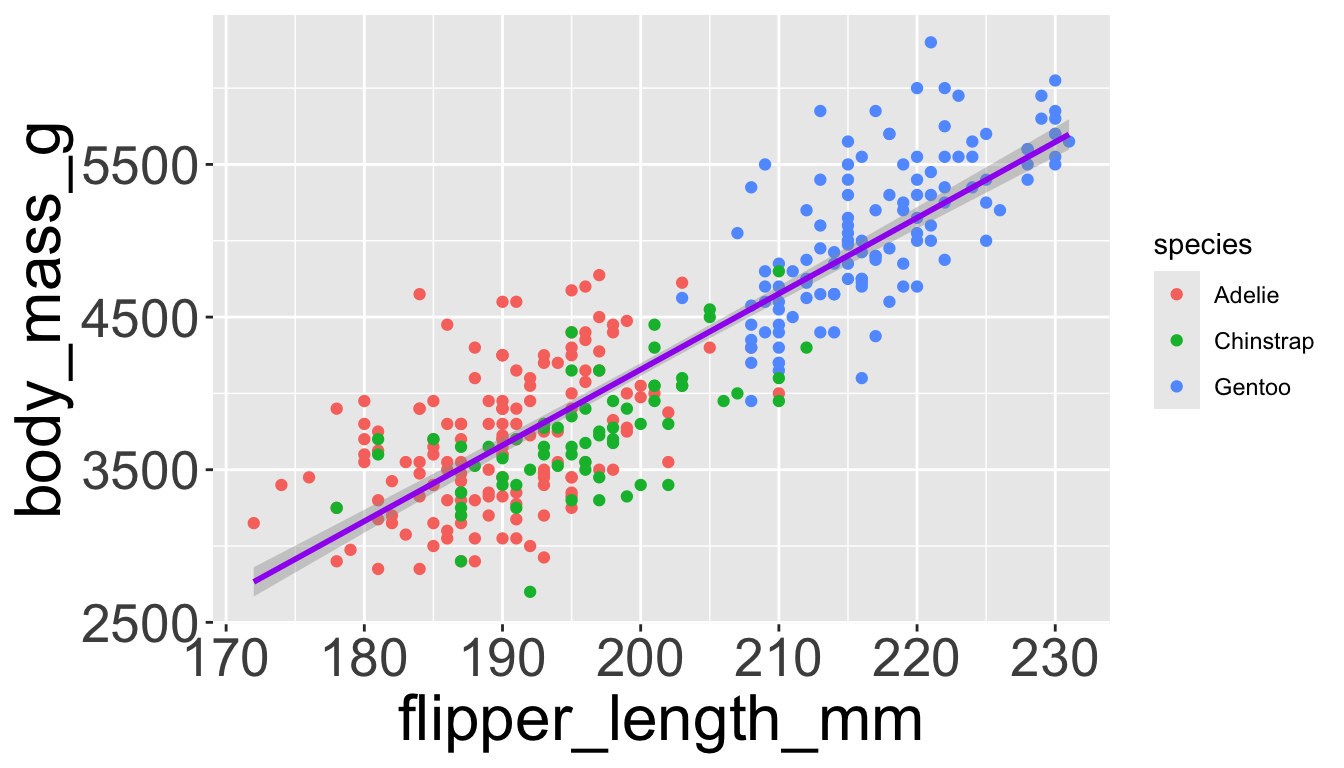
We can have aesthetics change as a function of variables inside the tibble

• e.g. we can differentiate penguin species via colors
• When a categorical variable is mapped to an aesthetic, each unique level of the variable (here: species) gets assigned a unique aesthetic value (here: unique color)

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g,
               color = species)) +
    geom_point()

Adding aesthetics and layers

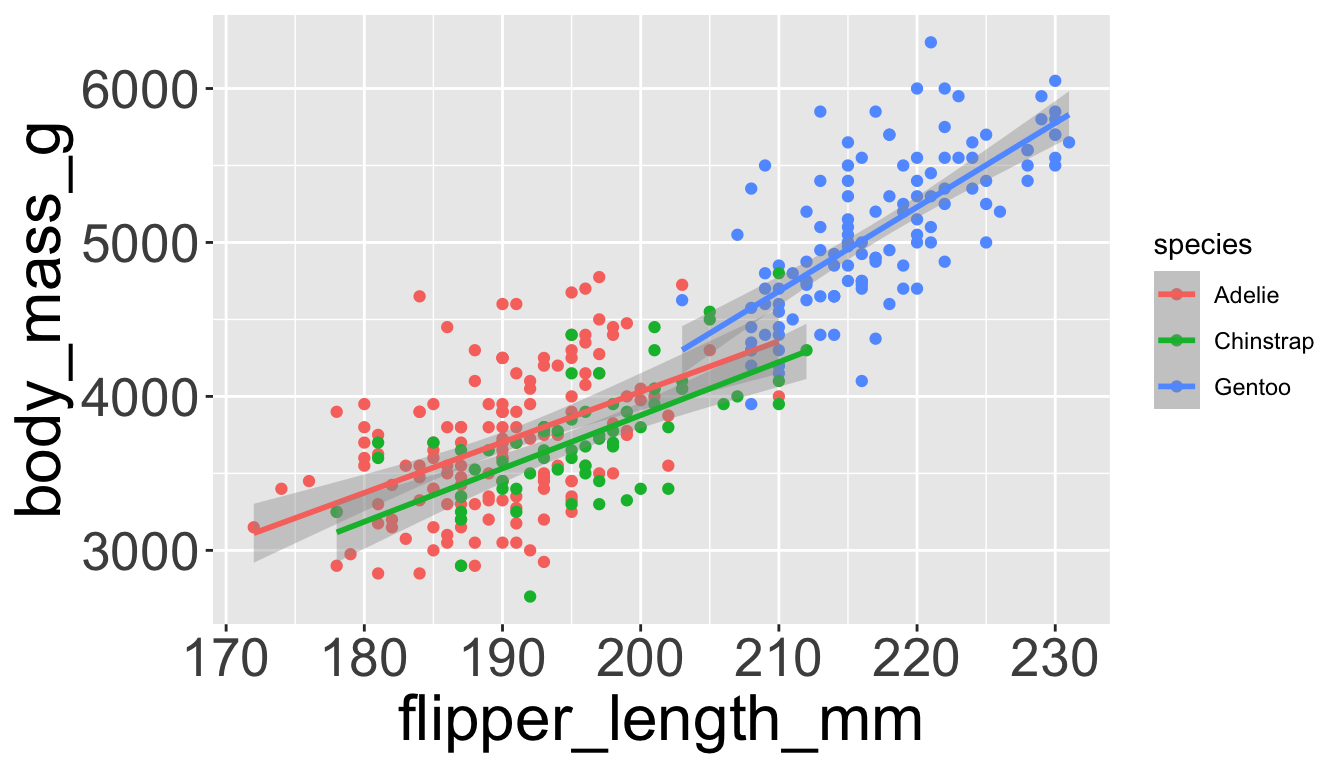
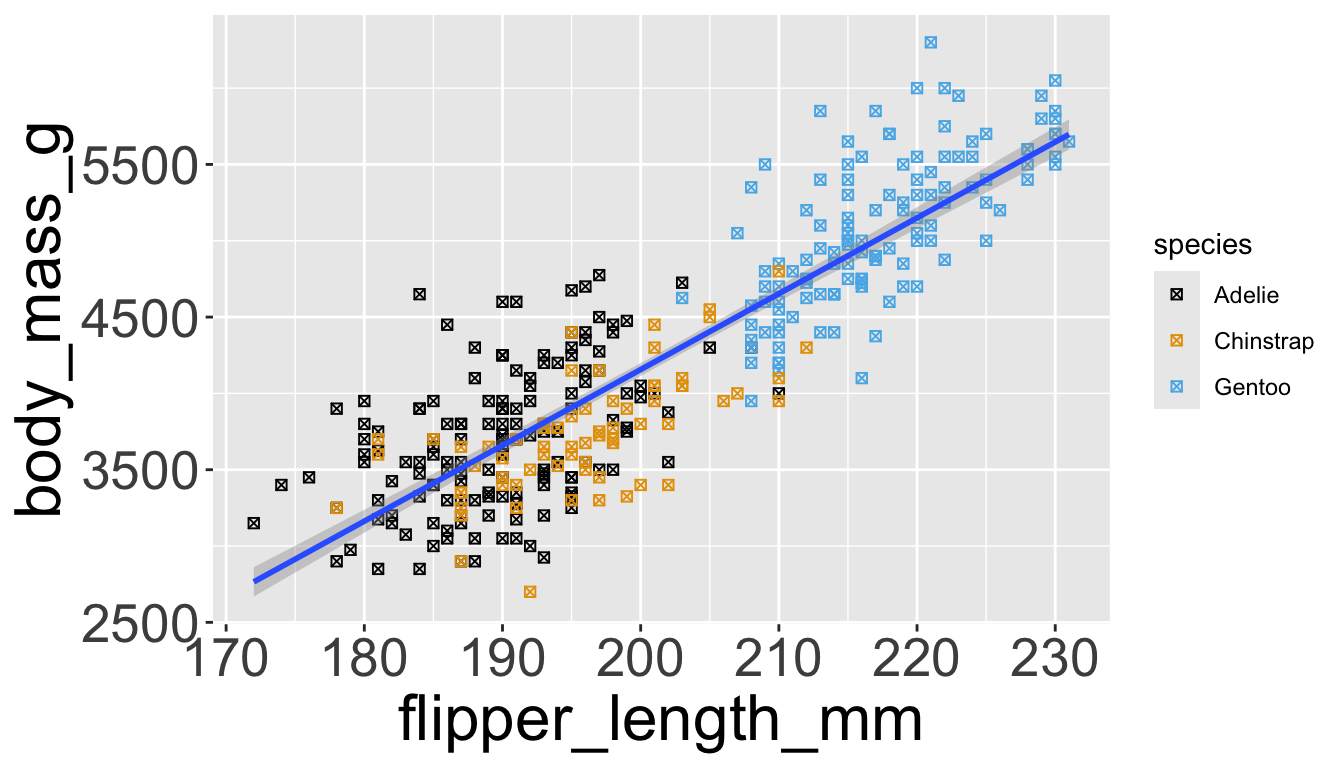
Let’s add a new layer, geom_smooth(method="lm"), which visualizes line of best fit based on a linear model

• When an aesthetic mapping is added inside ggplot(), it is applied to all layers.
  • So color=species inside ggplot() will group all penguins by species.
  • We now have a line for each species (not one global line).

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g,
               color = species)) +
    geom_point() + 
    geom_smooth(method = "lm")

Adding aesthetics and layers

Let’s add a new layer, geom_smooth(method="lm"), which visualizes line of best fit based on a linear model

• When an aesthetic mapping is added inside a layer, it is applied to just that layer.
  • So color=species inside geom_point() will group all penguins by species only for that layer.
  • We now have one global line for all penguins.

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(color = species)) + 
    geom_smooth(method = "lm", color = "purple")

Adding aesthetics and layers

Let’s make the colors more friendly to color-blind viewers

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(color = species)) + 
    geom_smooth(method = "lm", color = "purple") + 
    scale_color_colorblind()

Adding aesthetics and layers

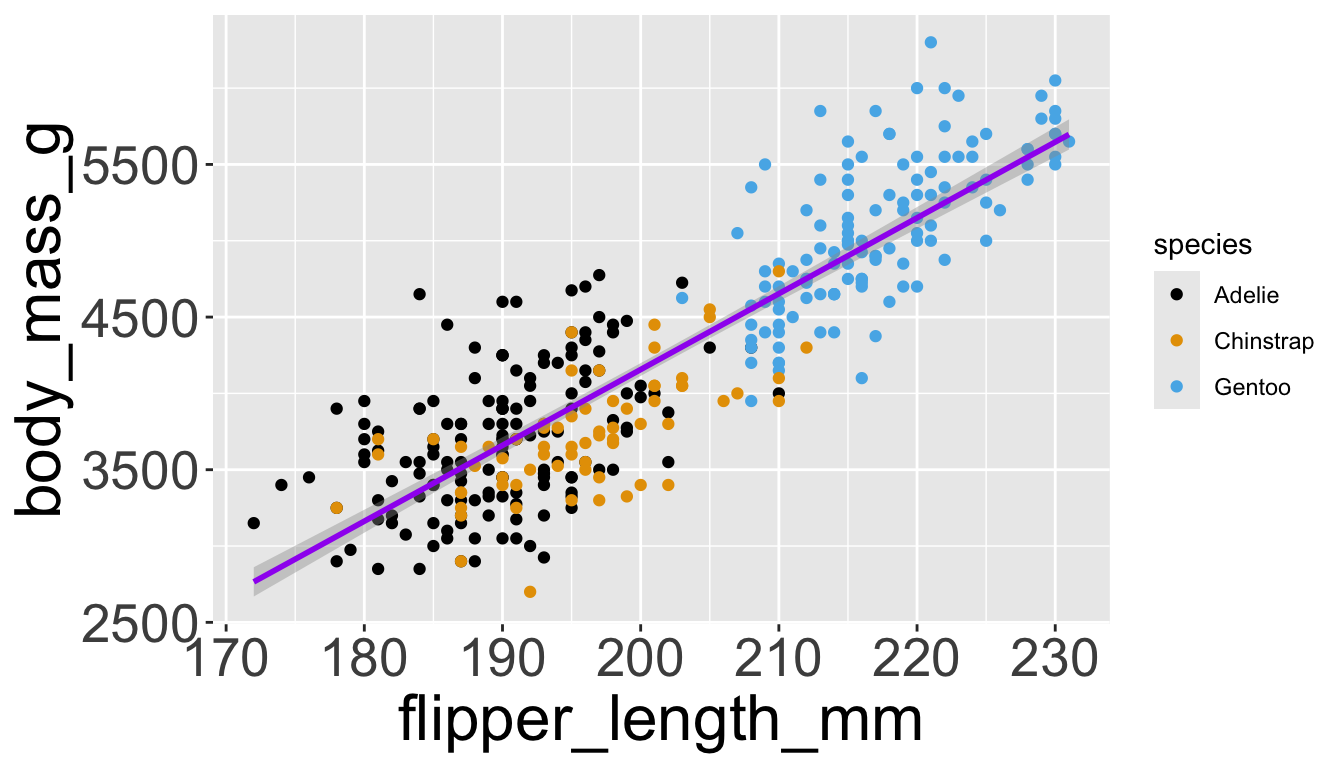
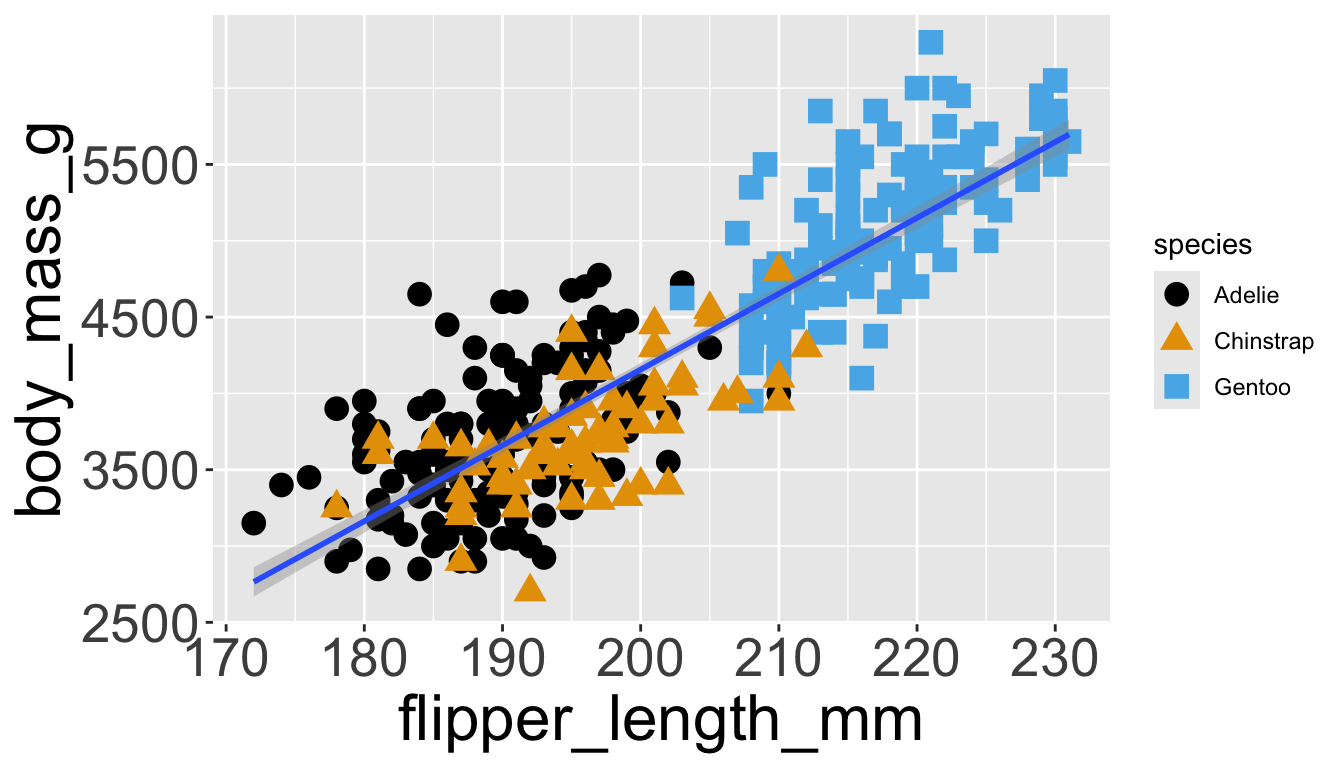
Let’s further differentiate different species via shapes.

• We can specify this in a local aesthetic mapping of points using shape=
• The legend will be updated to show this too!

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(color = species, 
                   shape = species)) + 
    geom_smooth(method = "lm", color = "purple") + 
    scale_color_colorblind()

Adding aesthetics and layers

Let’s further differentiate different species via shapes.

• We can make all points the same color by specifying color= outside of aes()

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(shape = species), 
               color = "orange") + 
    geom_smooth(method = "lm", color="black") + 
    scale_color_colorblind()

Adding aesthetics and layers

Let’s further differentiate different species via shapes.

• We can make all points the same shape by specifying shape= outside of aes()

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(color = species), 
               shape = 7) + 
    geom_smooth(method = "lm") + 
    scale_color_colorblind()

Adding aesthetics and layers

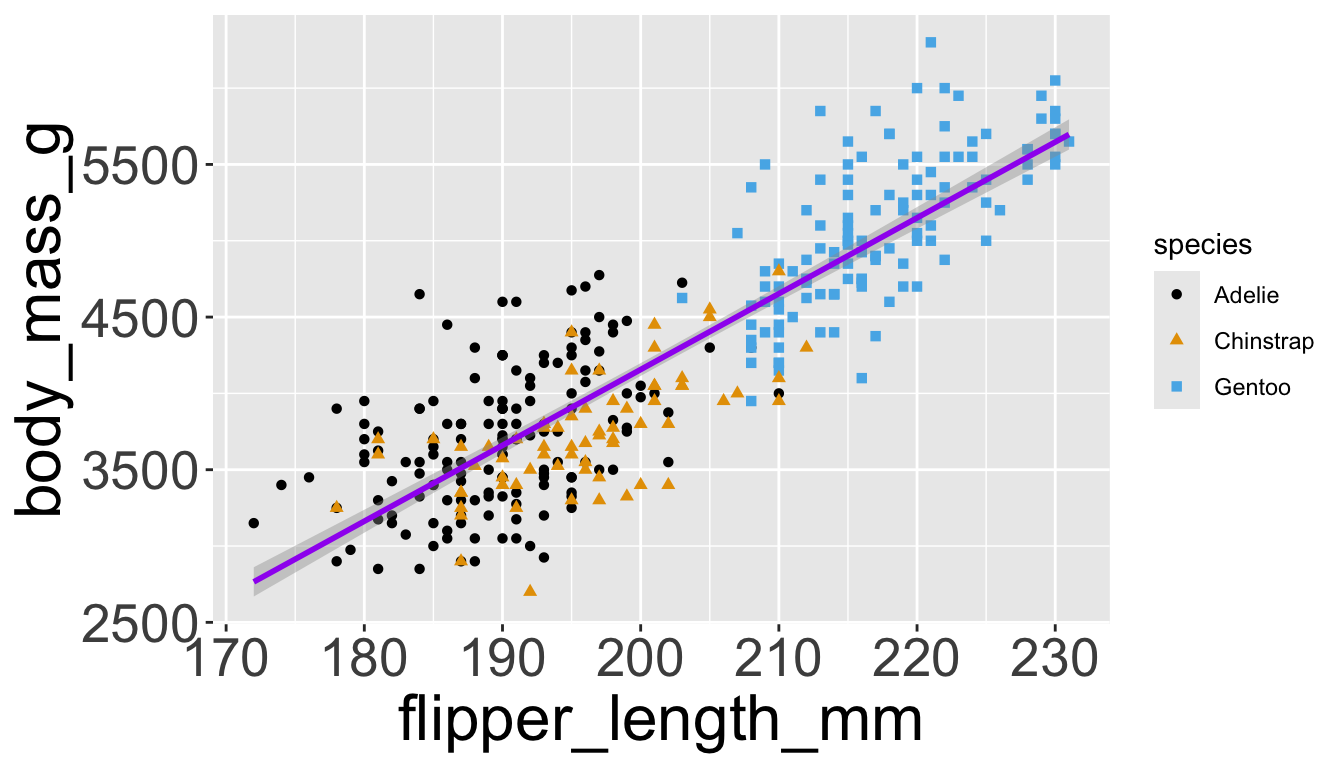
Let’s further differentiate different species via shapes.

• We can also specify shape= outside of aes()

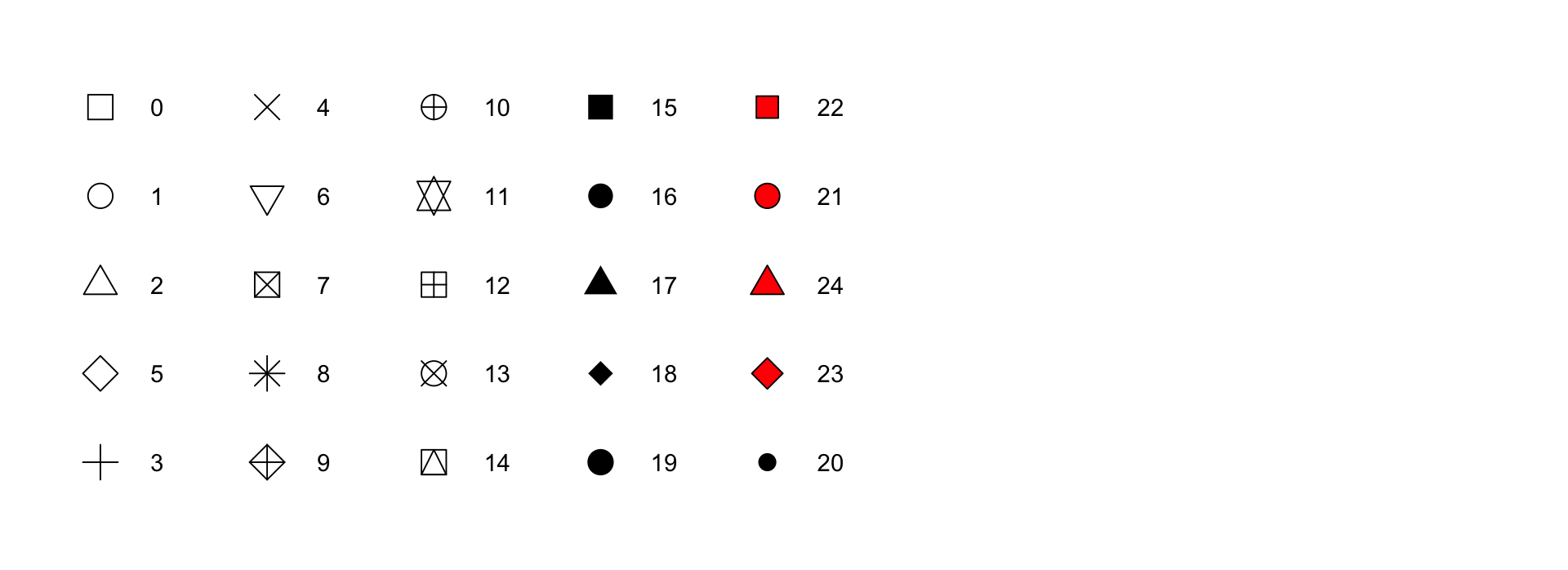
Figure 1: R has 25 built-in shapes that are identified by numbers. There are some seeming duplicates: for example, 0, 15, and 22 are all squares. The difference comes from the interaction of the color and fill aesthetics. The hollow shapes (0–14) have a border determined by color; the solid shapes (15–20) are filled with color; the filled shapes (21–24) have a border of color and are filled with fill.

Adding aesthetics and layers

Let’s further differentiate different species via shapes.

• We can also specify size= outside of aes()

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(color = species, 
                   shape = species), size=4) + 
    geom_smooth(method = "lm") + 
    scale_color_colorblind()

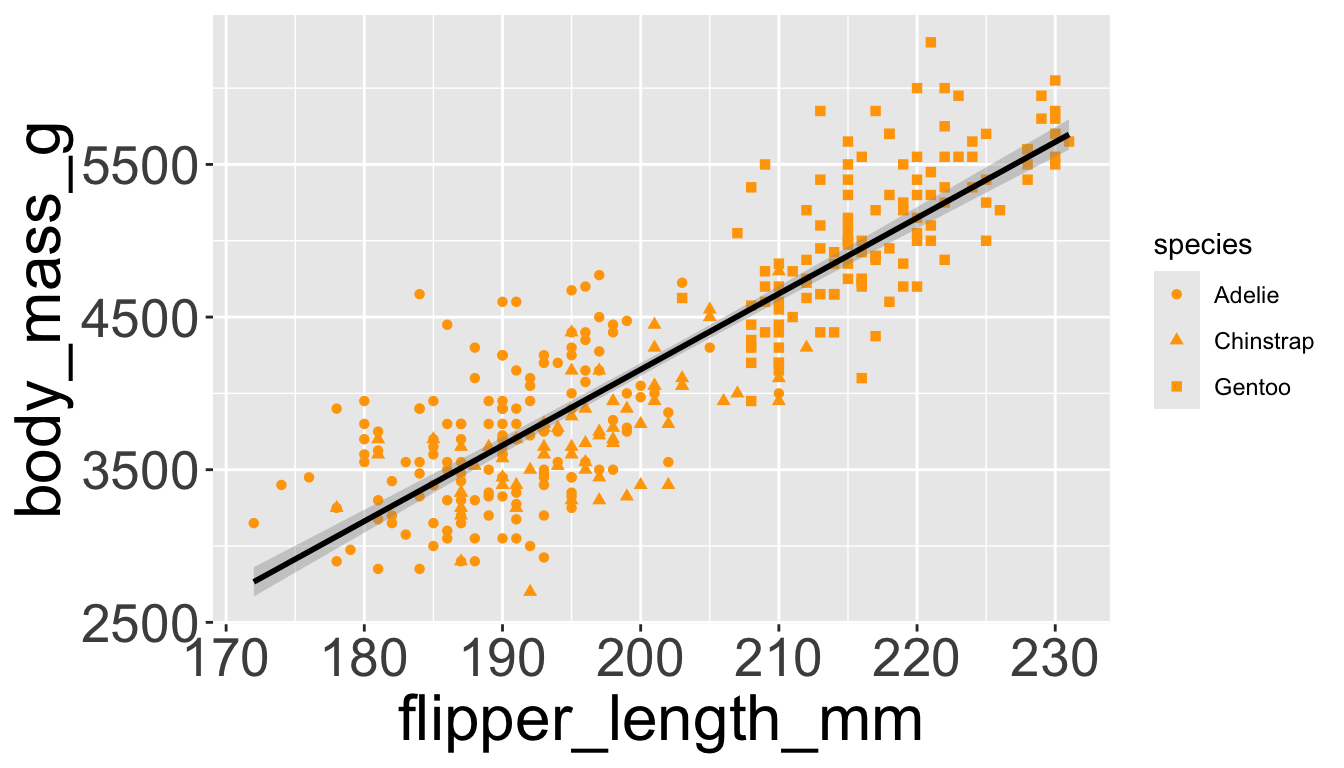
Now just need to add title and axis labels

penguins |> 
    ggplot(aes(x = flipper_length_mm,
               y = body_mass_g)) +
    geom_point(aes(color = species, 
                   shape = species)) + 
    geom_smooth(method = "lm") + 
  labs(
    title = "Body mass and flipper length",
    subtitle = "Dimensions for Adelie, Chinstrap, and Gentoo Penguins",
    x = "Flipper length (mm)", y = "Body mass (g)",
    color = "Species", shape = "Species"
  ) +
  scale_color_colorblind()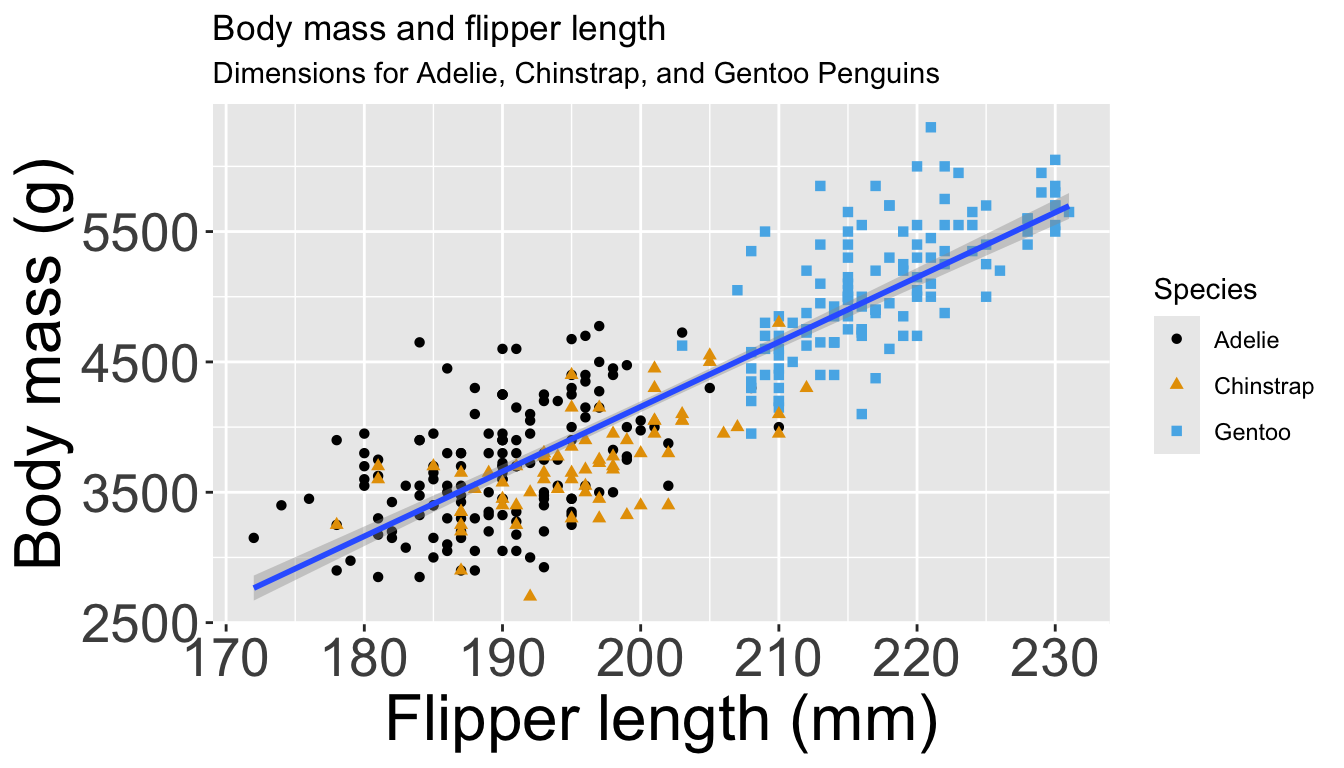

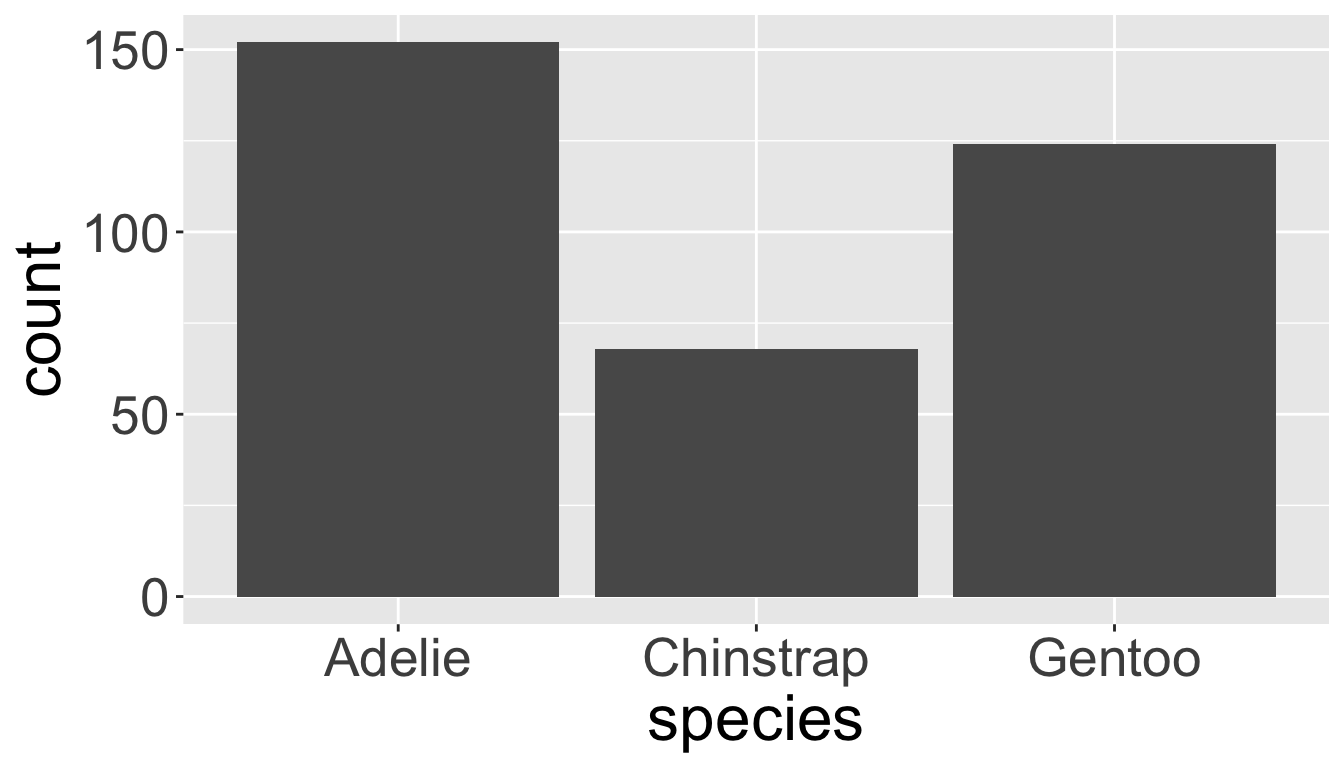
Visualizing distributions

Categorical variables take only one of a finite set of values

• Bar charts are useful for visualizing categorical variables

penguins |> 
    ggplot(aes(x = species)) +
    geom_bar()

Numeric values we are familiar with

• Histograms are useful for these - use argument binwidth =

penguins |> 
    ggplot(aes(x = body_mass_g)) +
    geom_histogram(binwidth = 200)

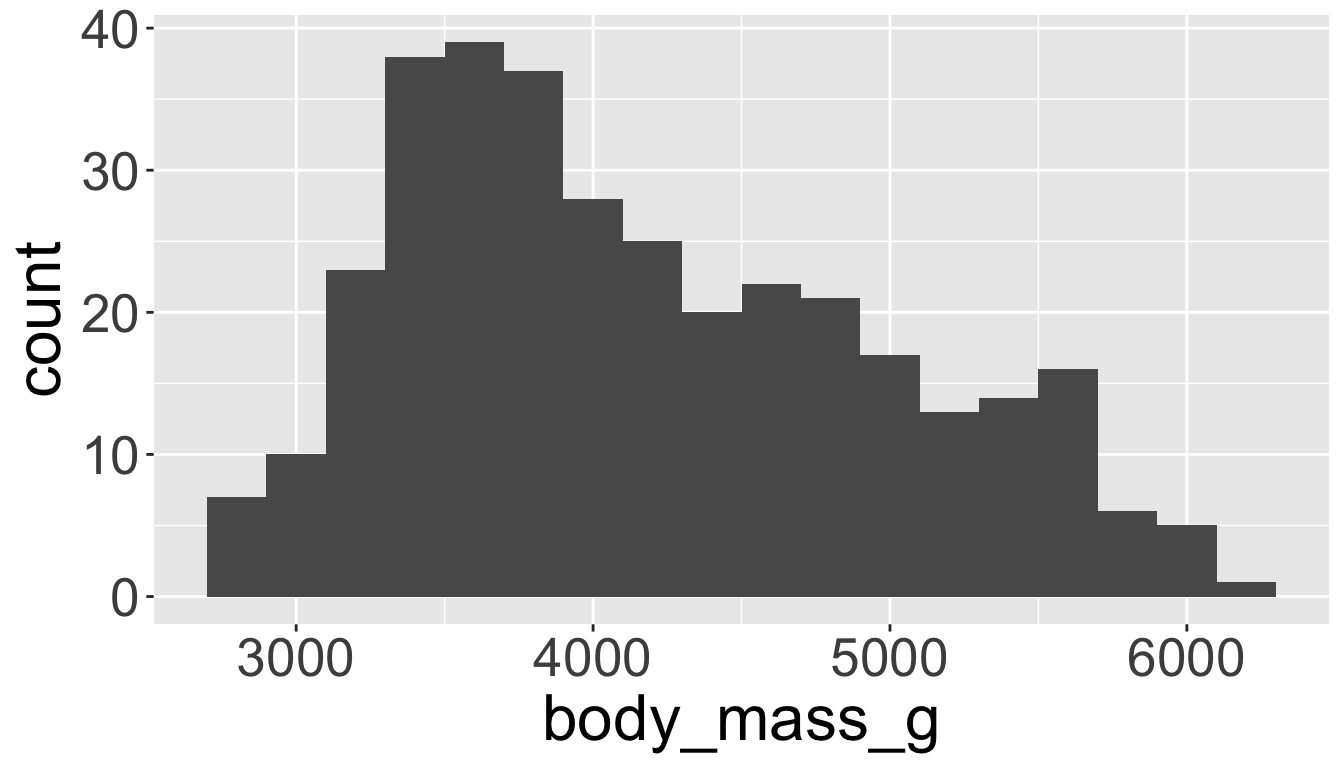
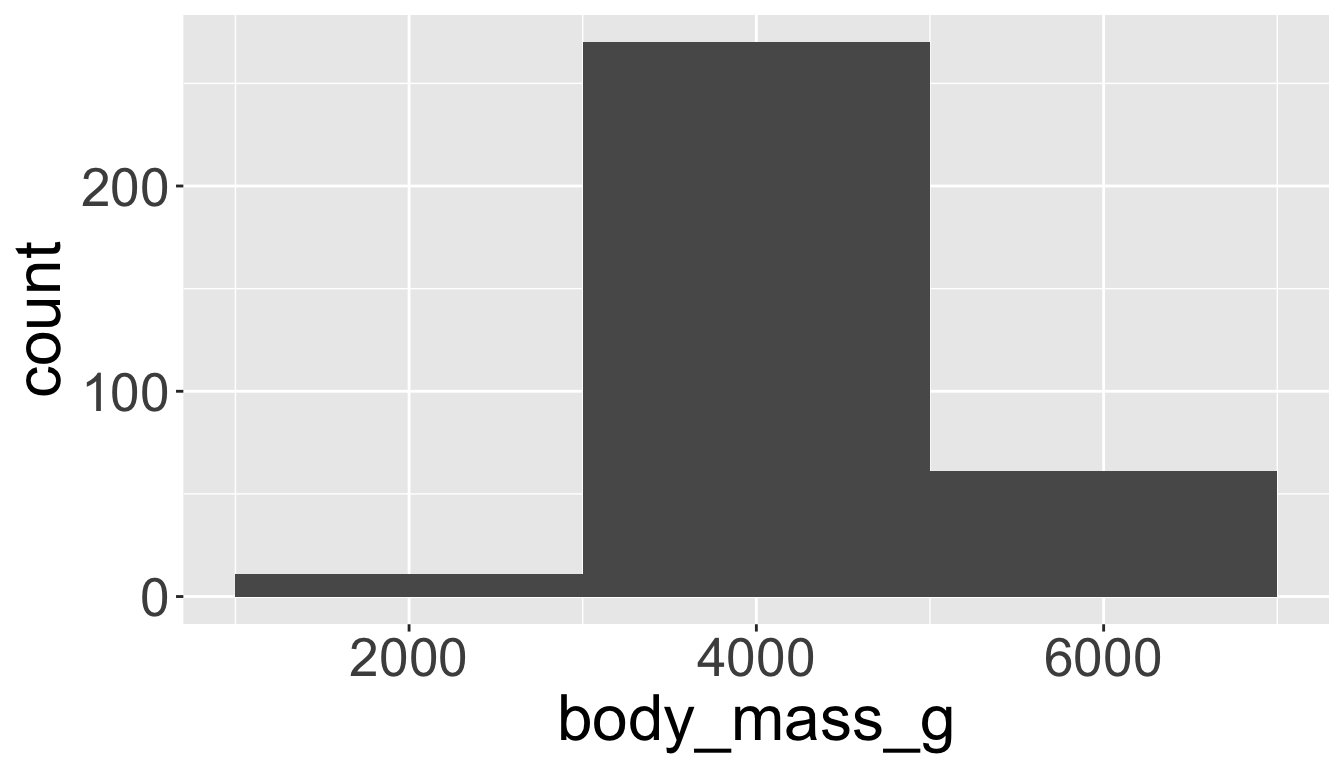
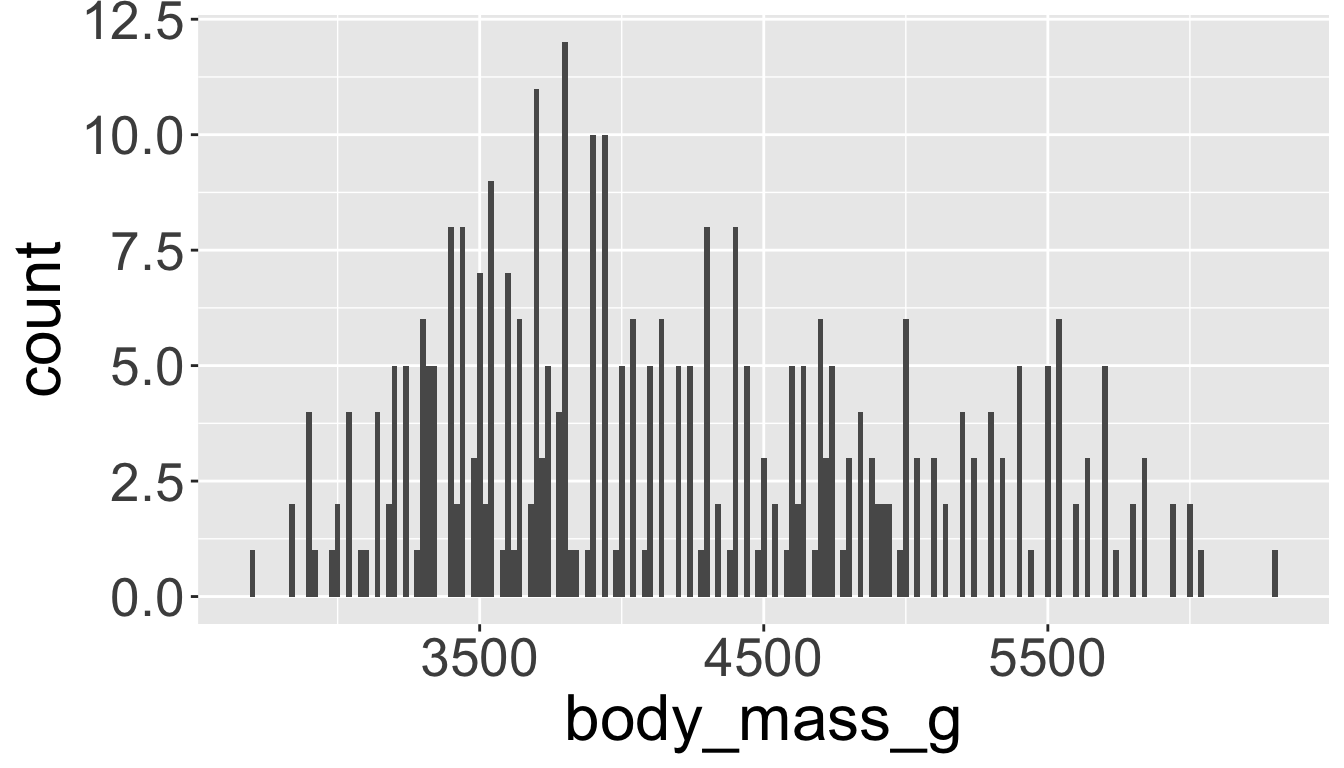
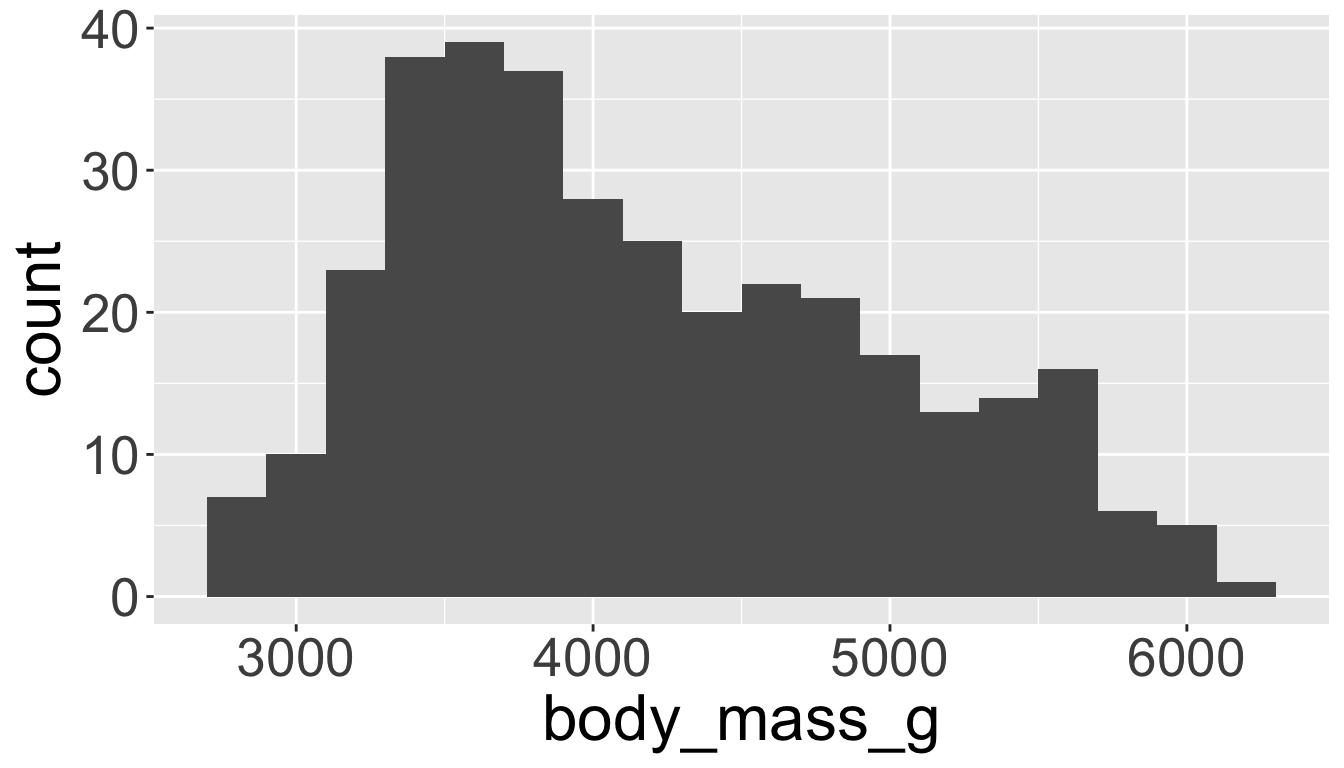
Visualizing distributions

You will likely need to spend time tuning the binwidth parameter

penguins |> 
    ggplot(aes(x = body_mass_g)) +
    geom_histogram(binwidth = 2000)

penguins |> 
    ggplot(aes(x = body_mass_g)) +
    geom_histogram(binwidth = 20)

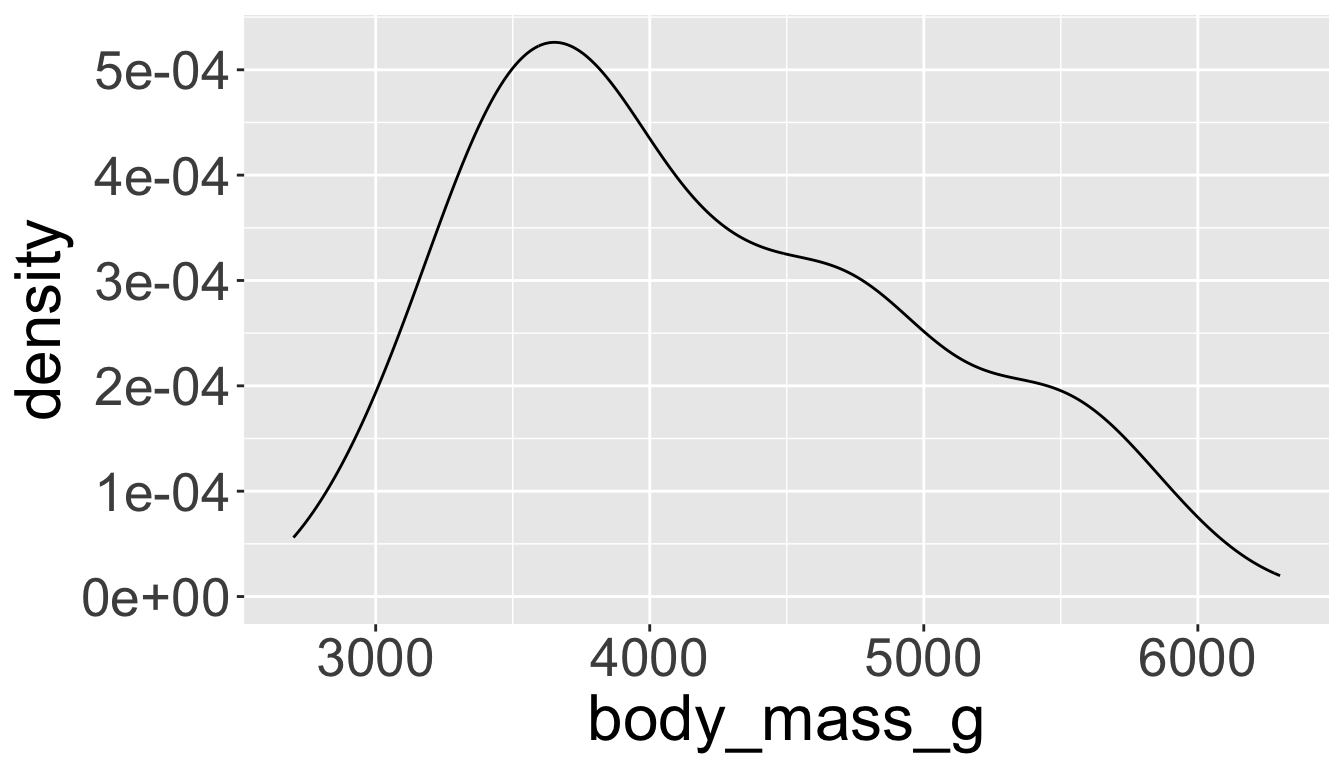
Visualizing distributions

• A smoothed out version of histogram which is supposed to approximate a probability density function

penguins |> 
    ggplot(aes(x = body_mass_g)) +
    geom_density()

penguins |> 
    ggplot(aes(x = body_mass_g)) +
    geom_histogram(binwidth = 200)

Visualizing distributions

• Let’s check the difference between setting color = vs fill = with geom_bar:

penguins |> 
    ggplot(aes(x = species)) +
    geom_bar(color = "red")

penguins |> 
    ggplot(aes(x = species)) +
    geom_bar(fill = "red")

Visualizing distributions

• Let’s check the difference between setting color = vs fill = with geom_bar:

penguins |> 
    ggplot(aes(x = species)) +
    geom_bar(color = "red")

penguins |> 
    ggplot(aes(x = species)) +
    geom_bar(fill = "red", color="purple")

Visualizing distributions

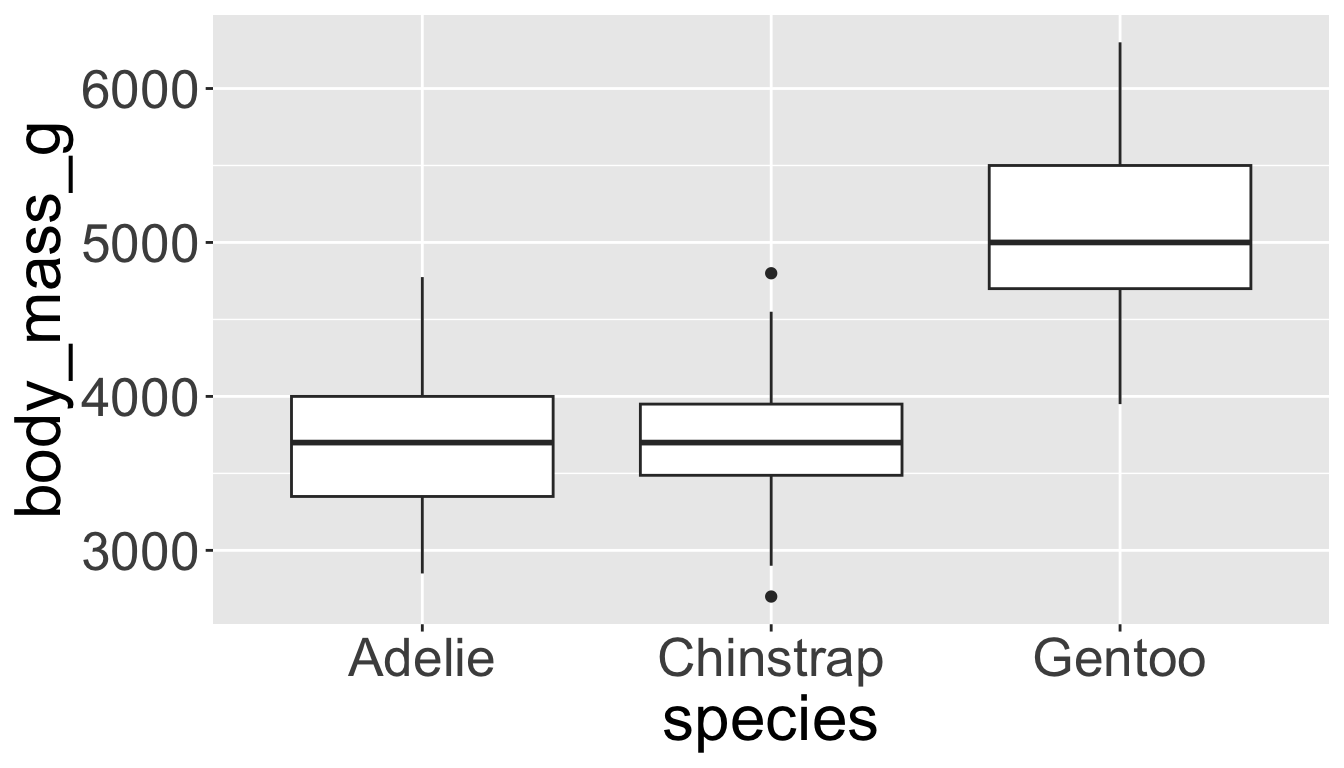
• Box plots allow for visualizing the spread of a distribution
• Makes it easy to see 25th percentile, median, 75th percentile, and outliers (>1.5*IQR from 25th or 75th percentile)

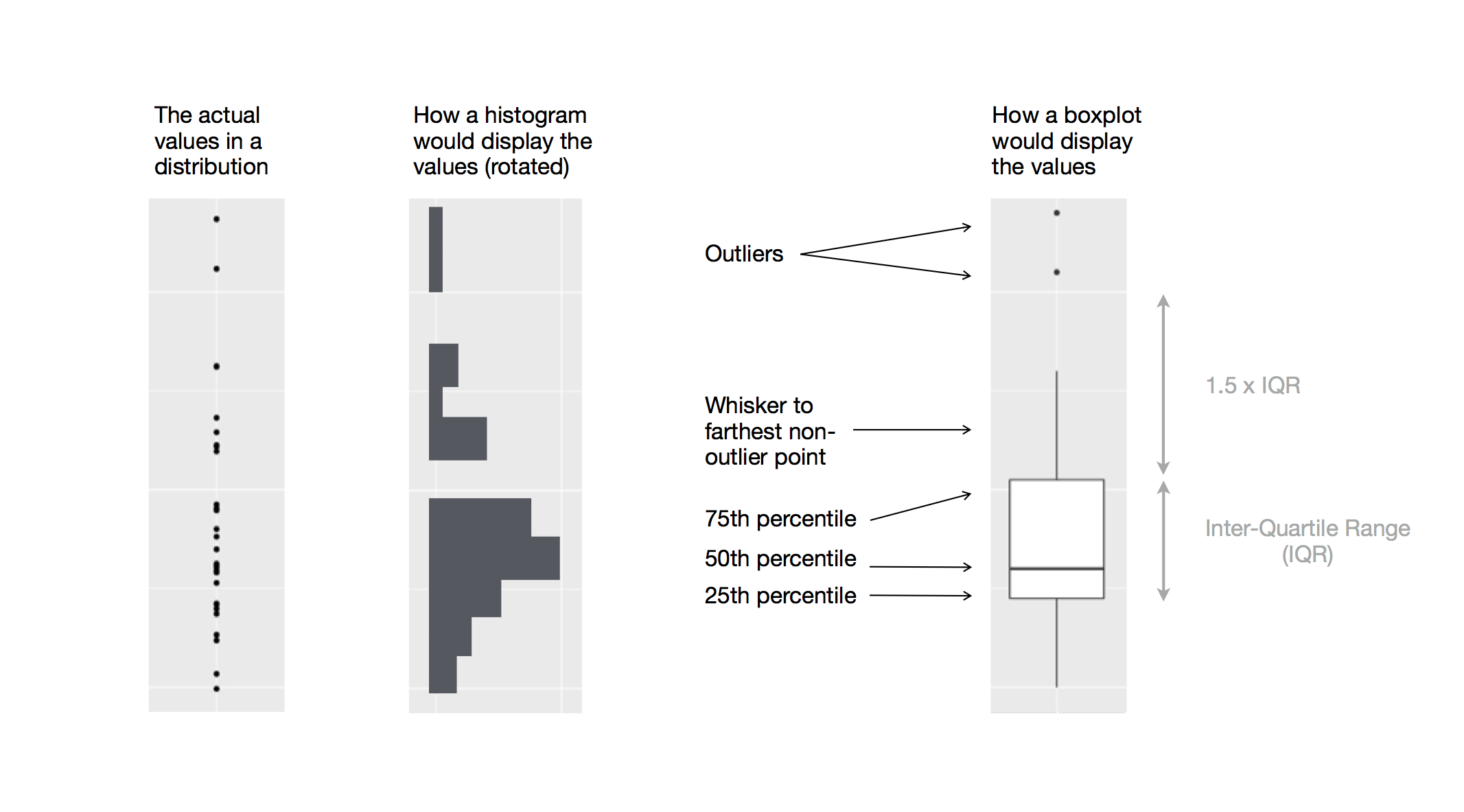
Visualizing distributions

Let’s see distribution of body mass by species…

…using geom_boxplot():

penguins |> 
    ggplot(aes(x = species, 
               y = body_mass_g)) +
    geom_boxplot()

…using geom_density():

penguins |> 
    ggplot(aes(x = body_mass_g, 
               color = species)) +
    geom_density(linewidth = 0.75)

Playing with visual parameters

Use alpha to add transparency

• alpha is a number between 0 and 1; 0 = transparent, 1 = opaque

penguins |> 
    ggplot(aes(x = body_mass_g, 
               color = species, 
               fill = species)) +
    geom_density(alpha = 0.3)

penguins |> 
    ggplot(aes(x = body_mass_g, 
               color = species, 
               fill = species)) +
    geom_density(alpha = 0.7)

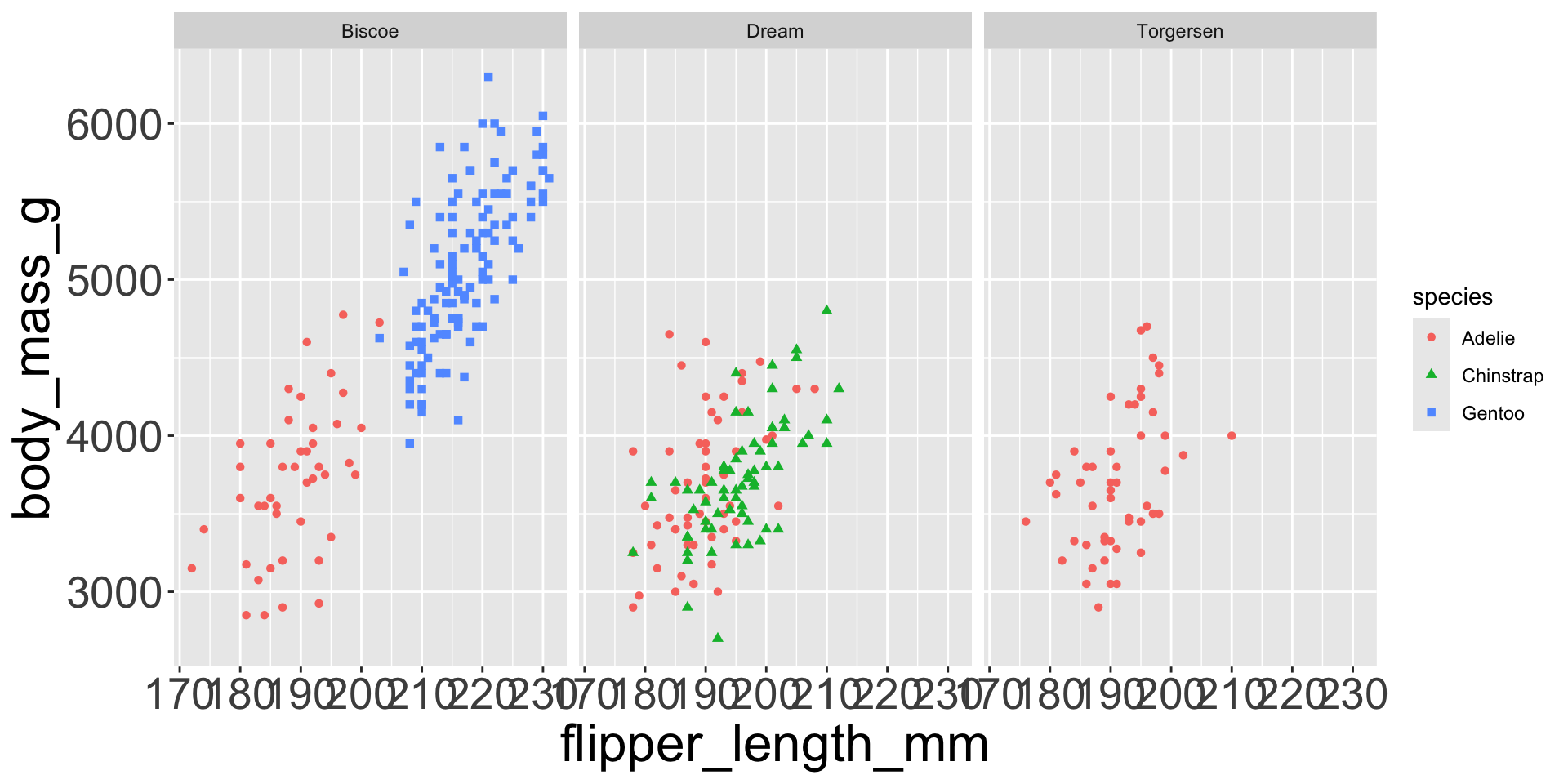
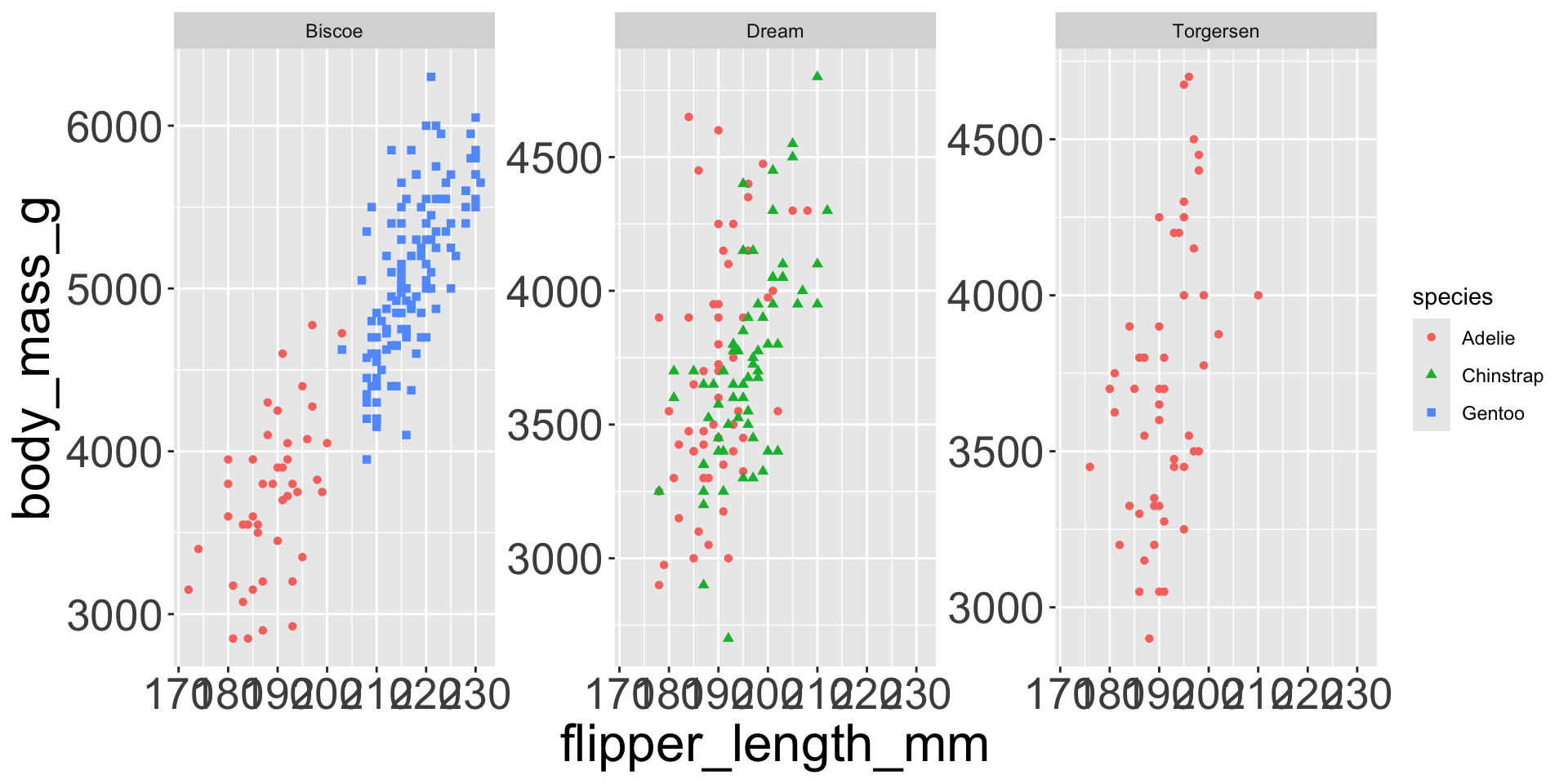
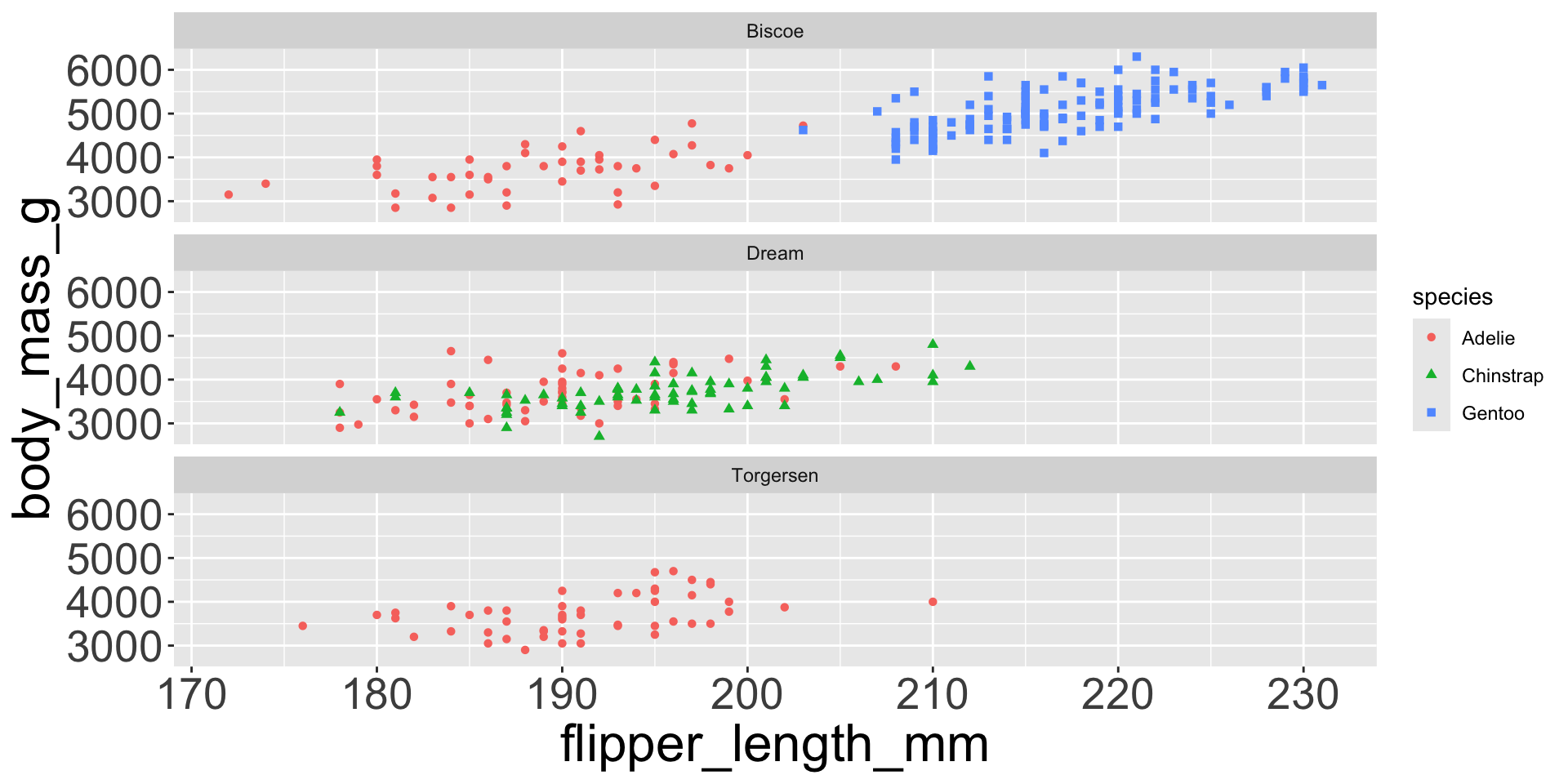
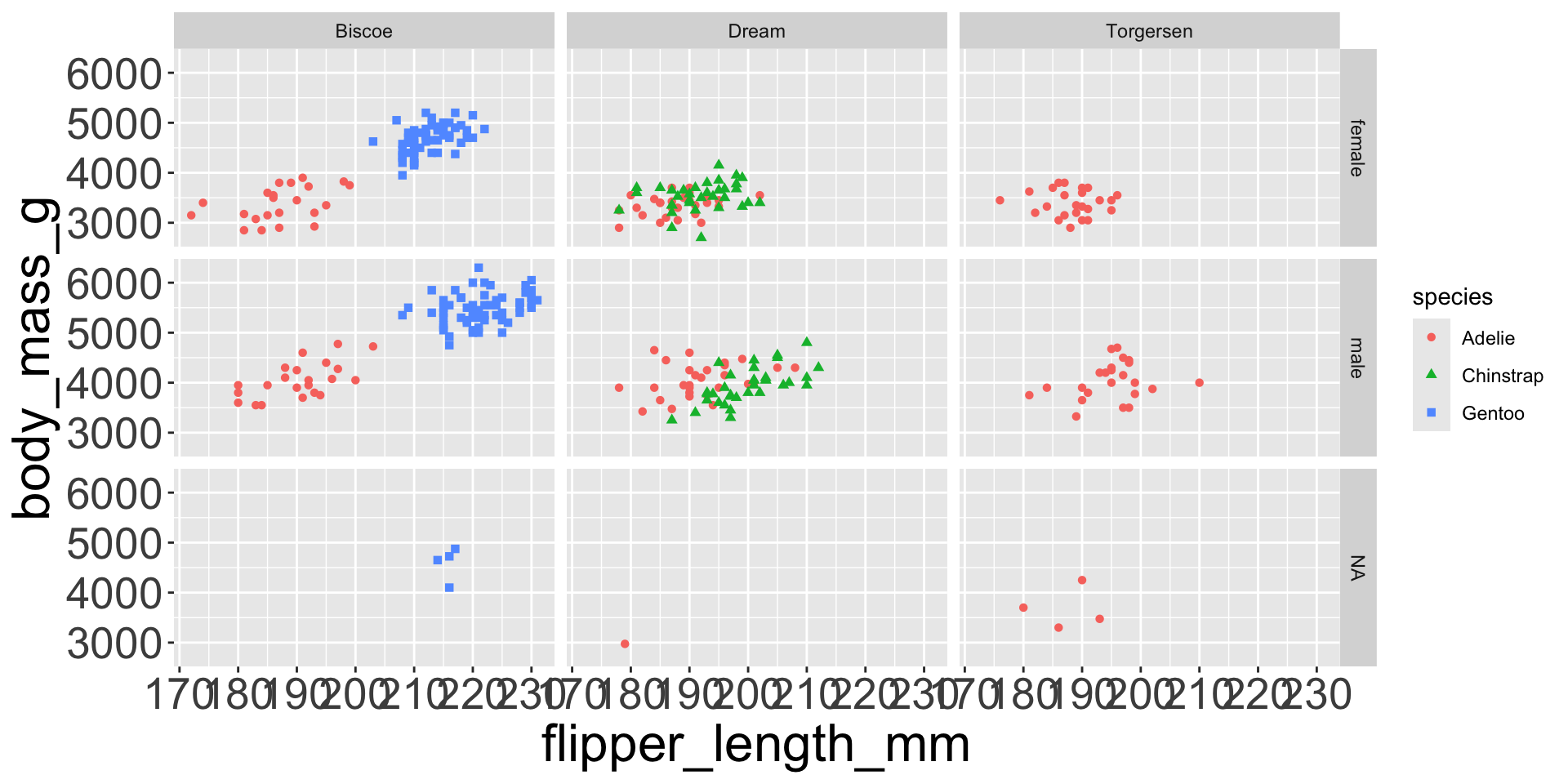
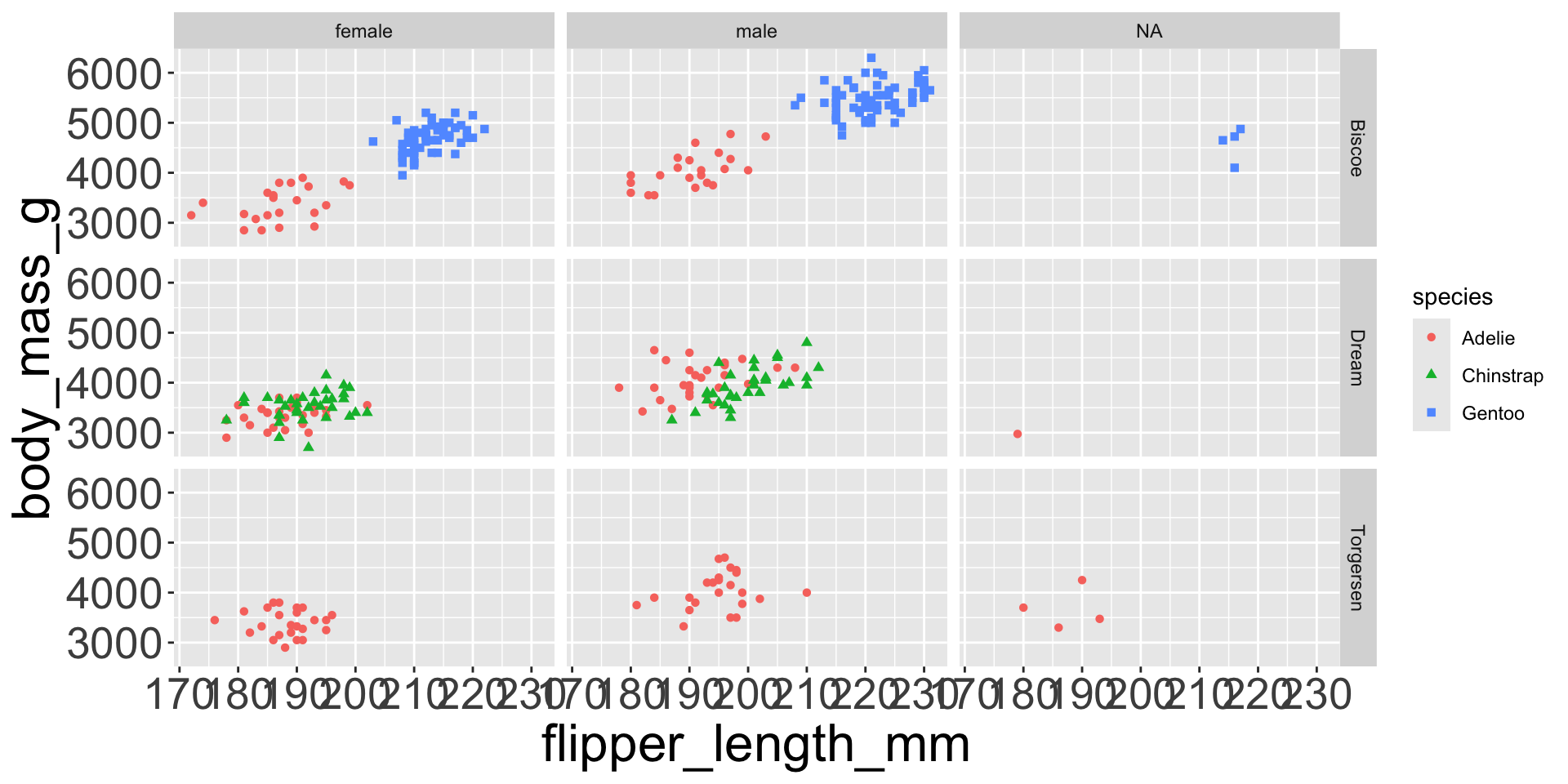
Multiple numerical variables

Already saw how to use scatter plots to visualize two numeric variables

We can use separate vals for color and shape

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = island))

Too many things to remember…

Multiple numerical variables

Too many aesthetic changes (shape, color, fill, size, etc) can clutter plots

• Can use facets
• facet_wrap() takes a formula argument

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_wrap(~island)

Multiple numerical variables

Too many aesthetic changes (shape, color, fill, size, etc) can clutter plots

• Can use facets
• facet_wrap() takes a formula argument

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_wrap(~island, scales="free_y")  # each panel now has its own y-axis scale

Multiple numerical variables

Too many aesthetic changes (shape, color, fill, size, etc) can clutter plots

• Can use facets
• facet_wrap() takes a formula argument

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_wrap(~island, ncol=1)

Multiple numerical variables

Too many aesthetic changes (shape, color, fill, size, etc) can clutter plots

• Can use facets
• facet_wrap() takes a formula argument

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_wrap(~island, ncol=2, nrow=2)

Multiple numerical variables

Too many aesthetic changes (shape, color, fill, size, etc) can clutter plots

• Can use facets
• facet_grid() takes a formula argument

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_grid(sex~island)

Multiple numerical variables

Too many aesthetic changes (shape, color, fill, size, etc) can clutter plots

• Can use facets
• facet_grid() takes a formula argument

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_grid(island~sex)

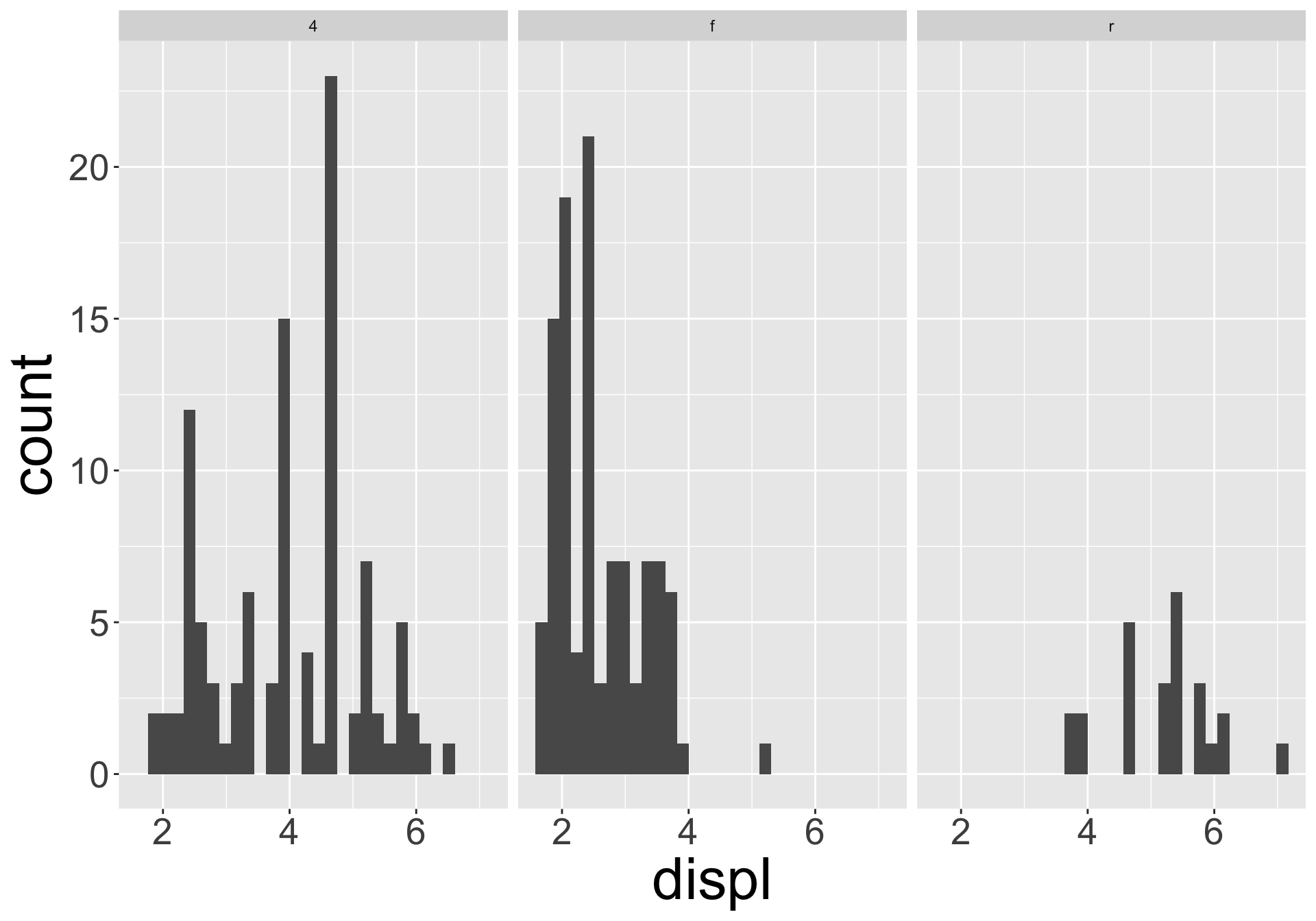
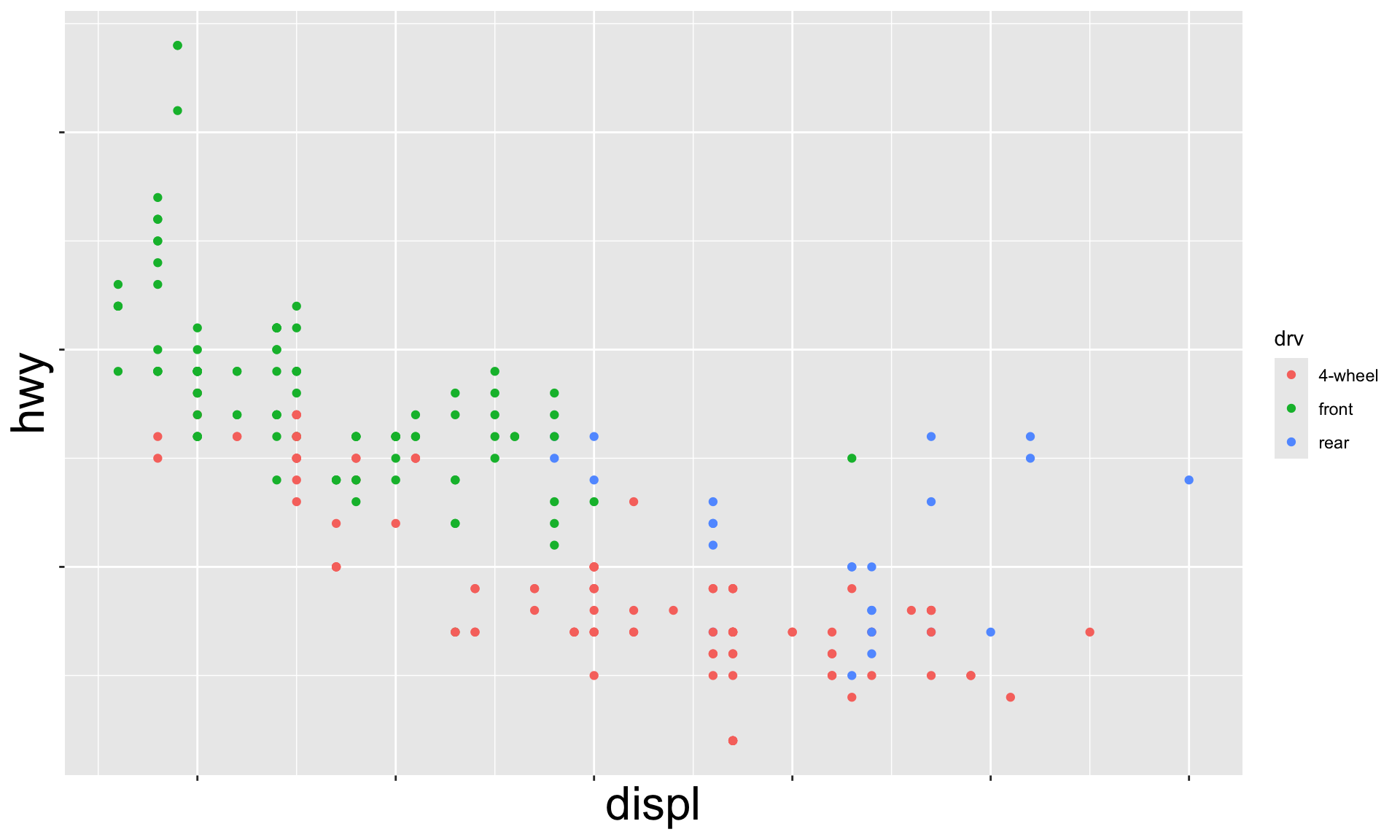
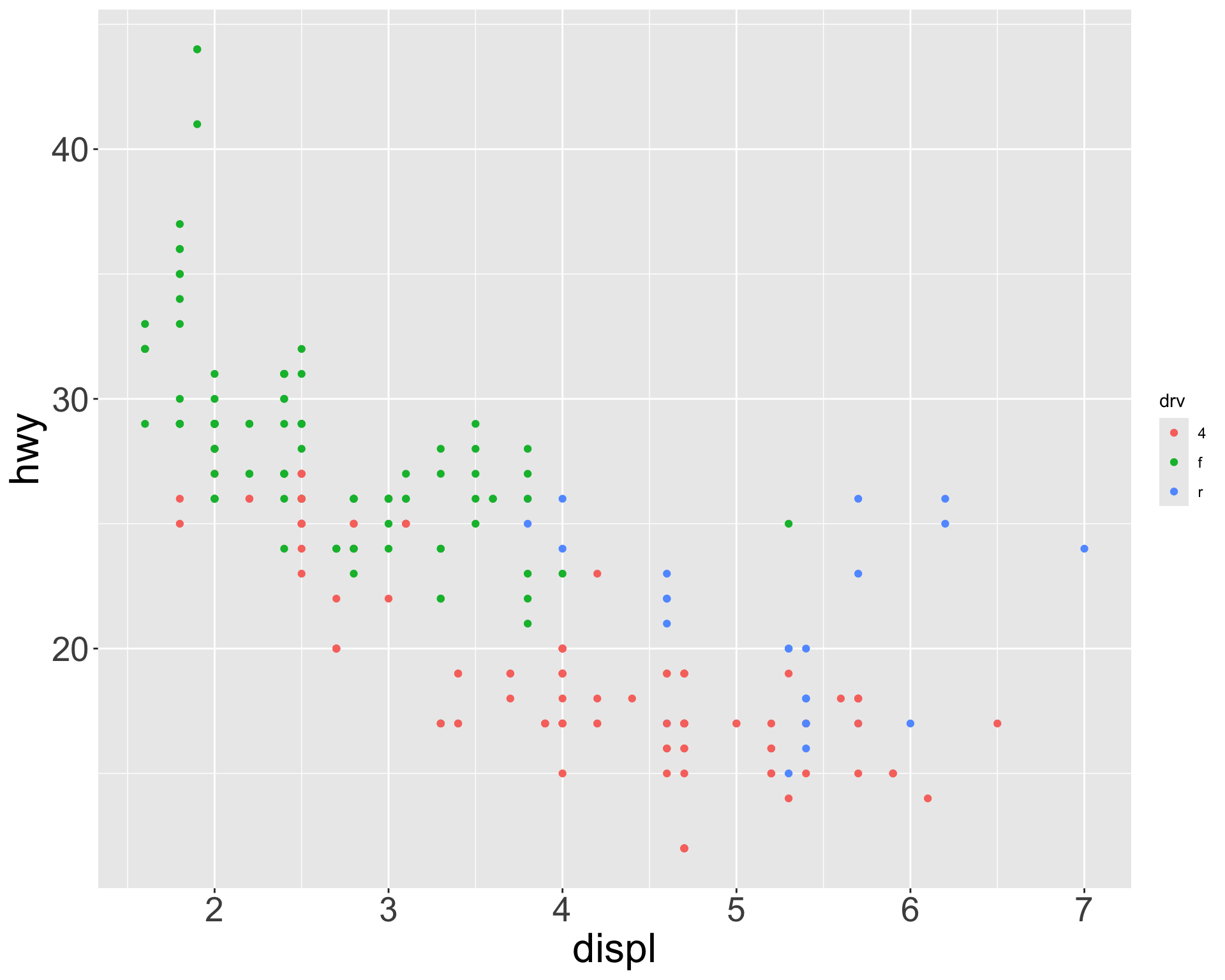
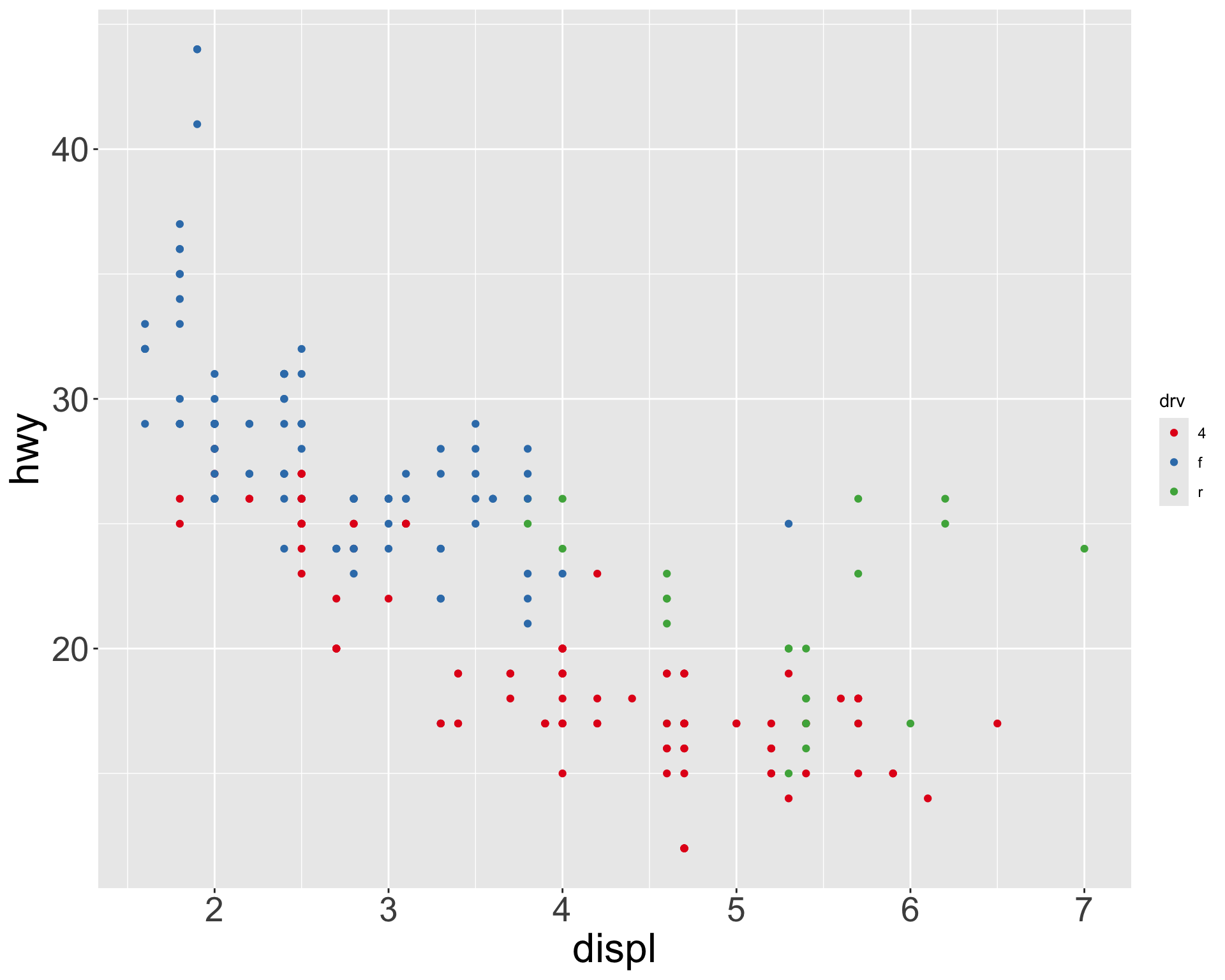
Multiple numerical variables

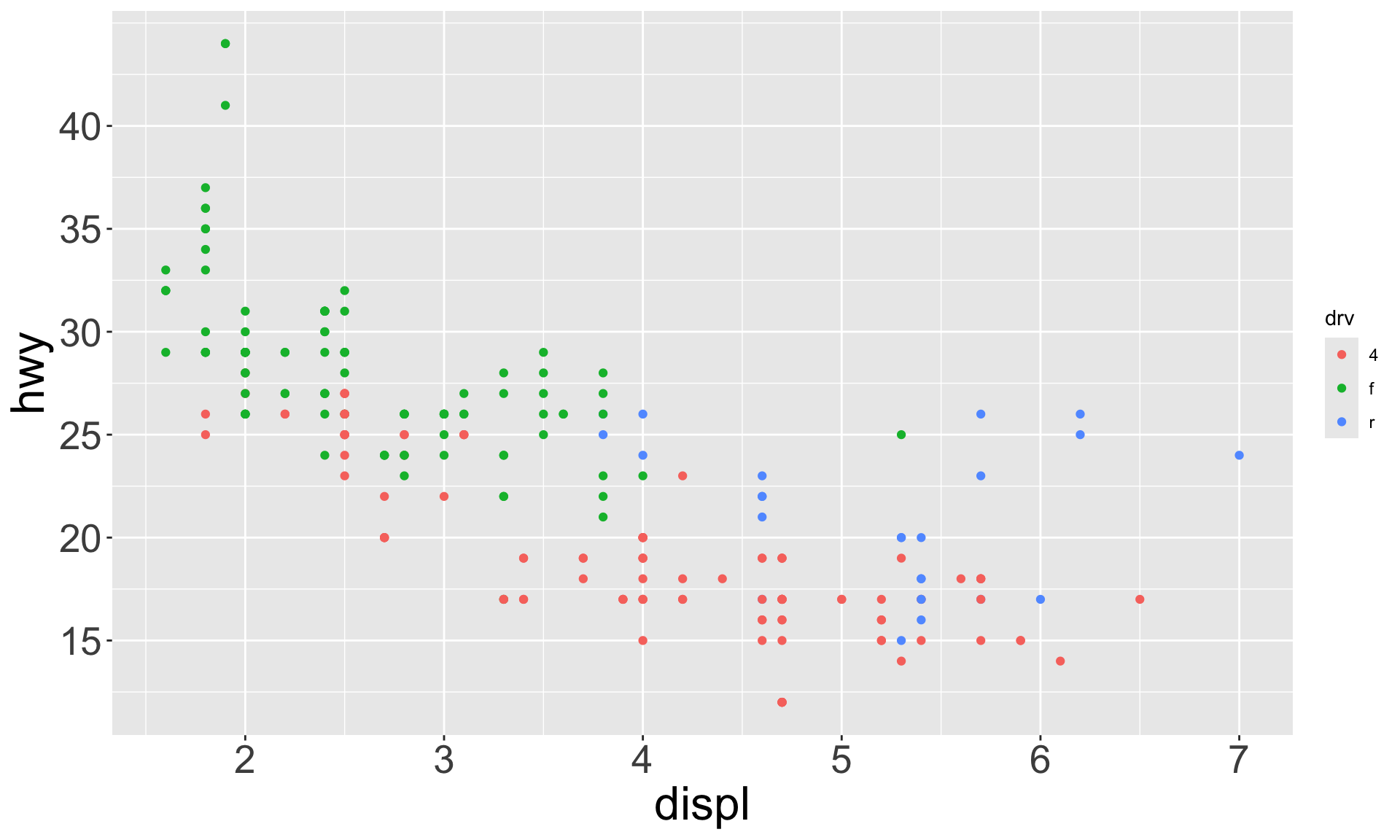
Which of the following makes it easier to compare engine size (displ) across cars with different drive trains?

ggplot(mpg, aes(x = displ)) + 
  geom_histogram() + 
  facet_wrap(~ drv, ncol=1) + 
  theme(axis.title = element_text(size=32), 
        axis.text = element_text(size=20))

ggplot(mpg, aes(x = displ)) + 
  geom_histogram() +
  facet_wrap(~ drv, nrow=1) + 
  theme(axis.title = element_text(size=32), 
        axis.text=element_text(size=20))

Can change order of levels in factors

penguins |>
    mutate(island = factor(island, levels=c("Dream", "Biscoe", "Torgersen"))) |>
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species)) +
    facet_wrap(~island)

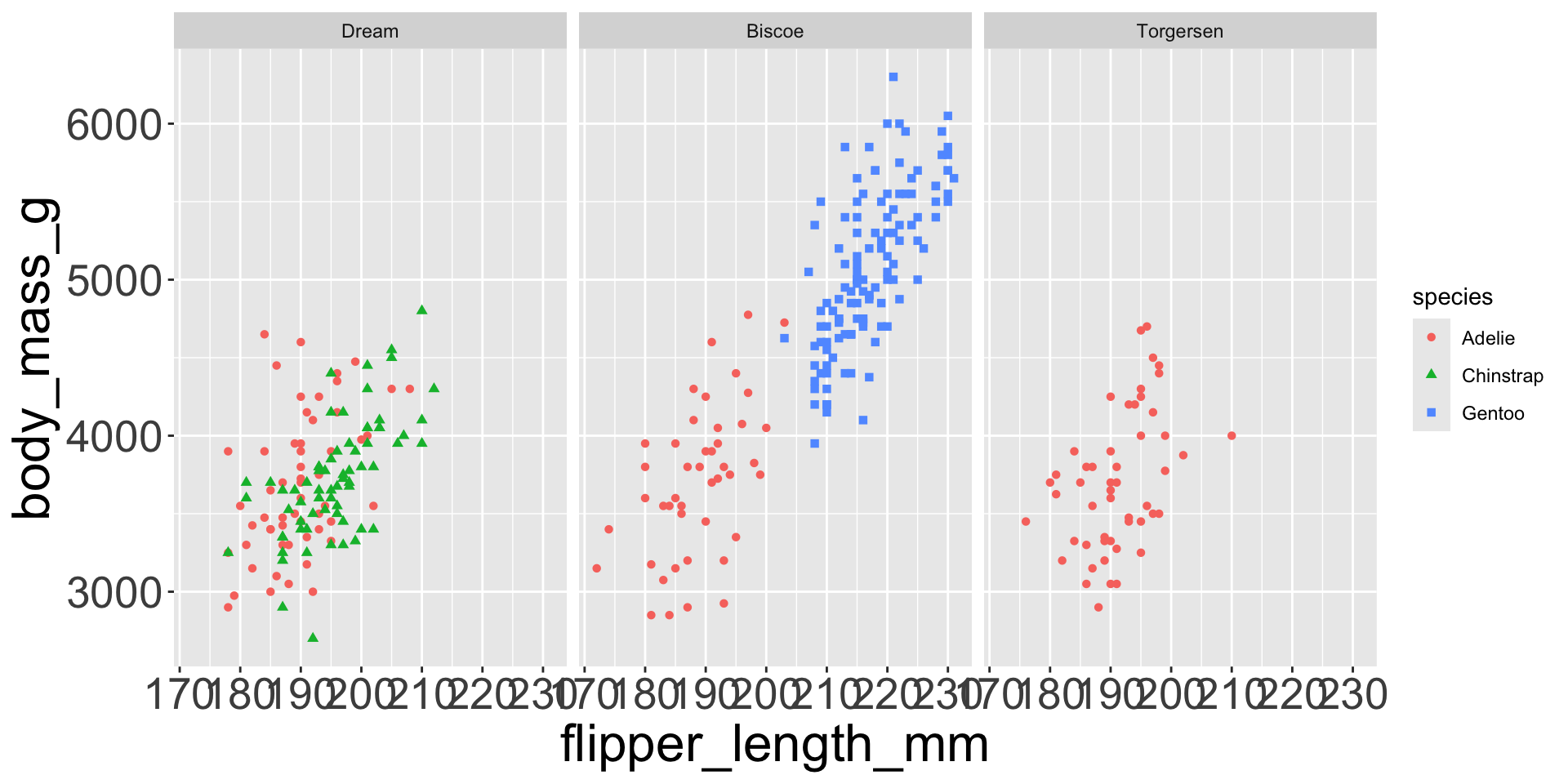
Shapes can be difficult to distinguish

penguins |>
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point(aes(color = species, shape = species))

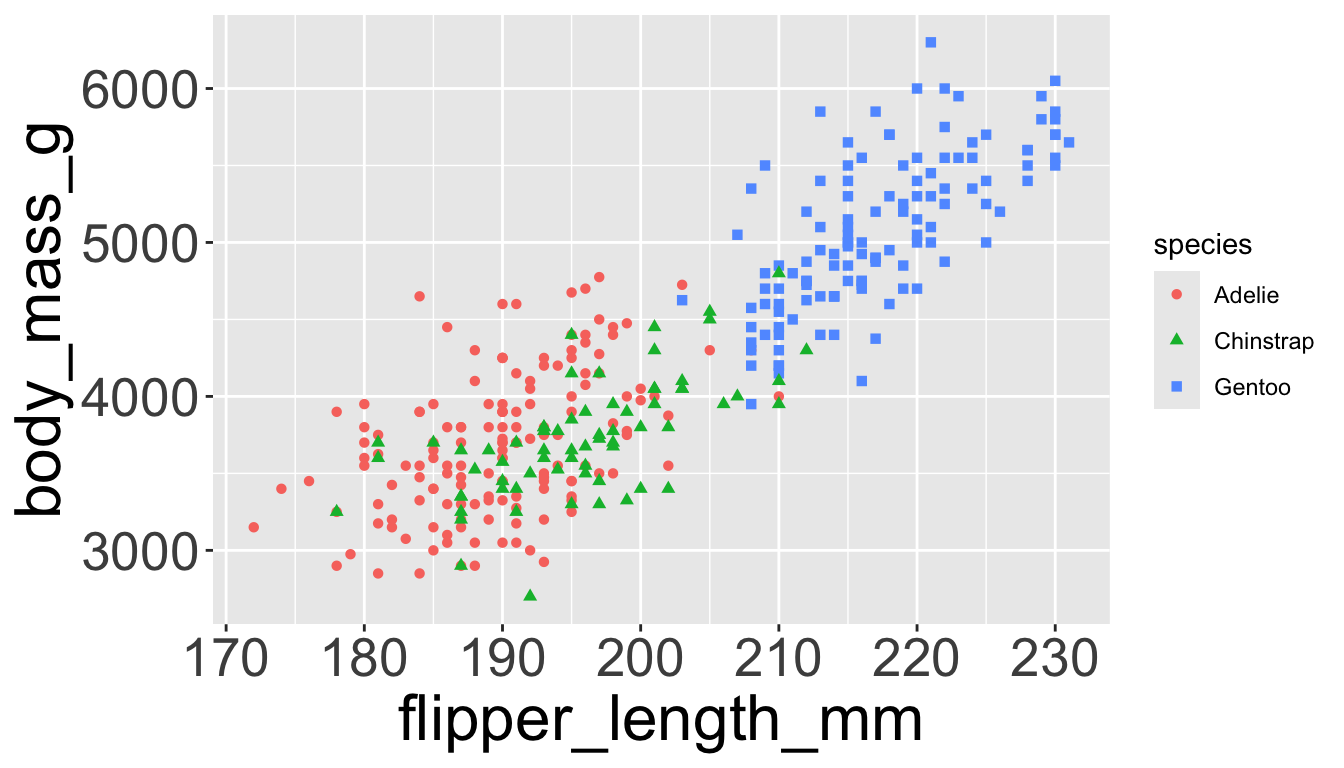
Sometimes easier to read by replacing shape with first letter

penguins |>
    mutate(species_first_letter = substr(species, 1, 1)) |>
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_text(aes(color = species, label = species_first_letter))

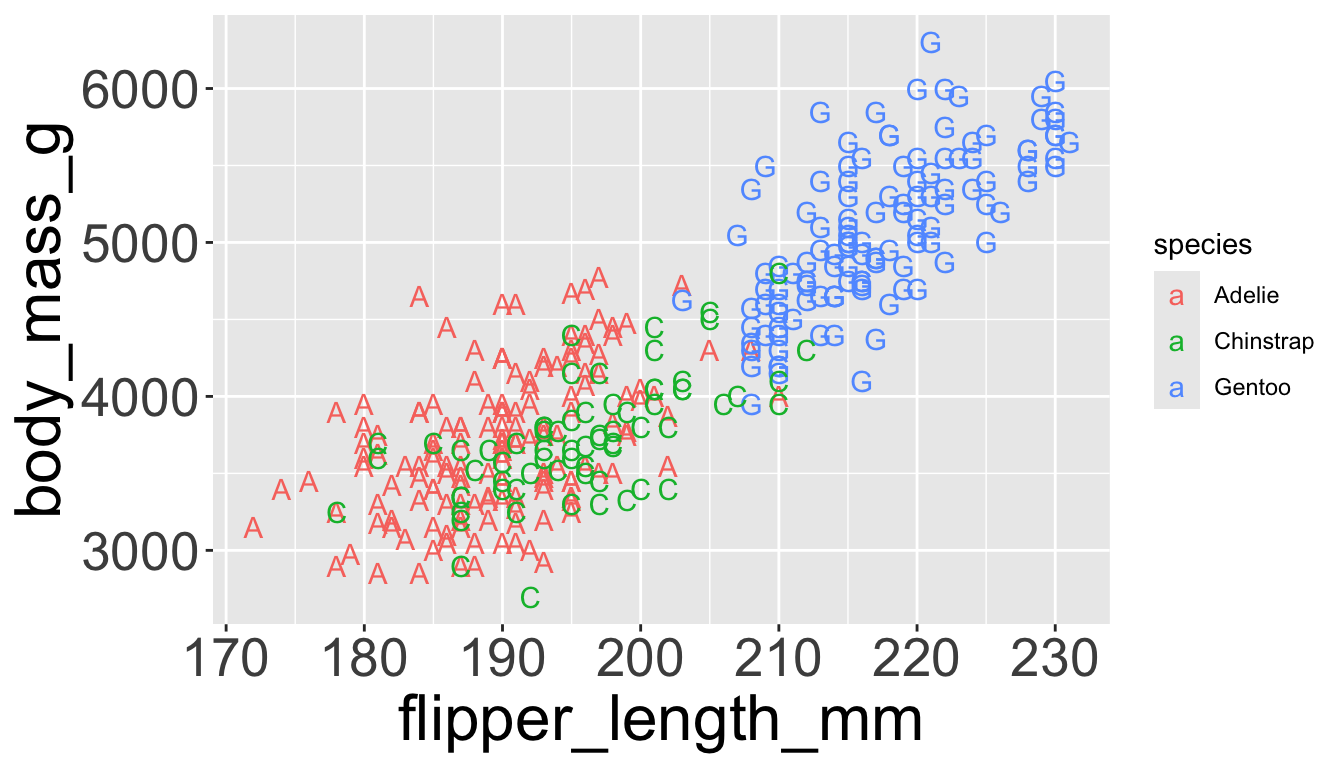
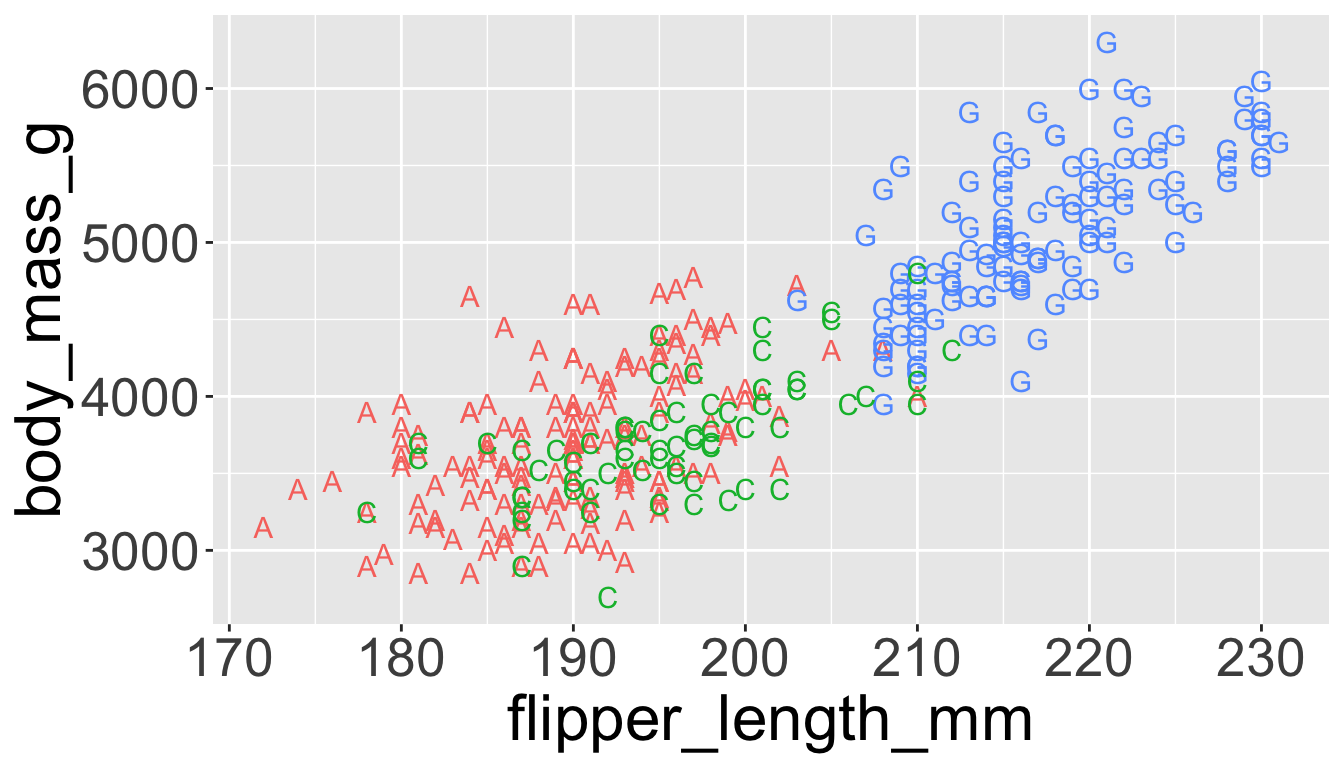
Might allow you to remove the legend

penguins |>
    mutate(species_first_letter = substr(species, 1, 1)) |>
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_text(aes(color = species, label = species_first_letter)) +
    theme(legend.position = "none")

Saving plots

Once you’ve made a plot, you can save using ggsave()

• Either can save whatever plot you made last:

penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point()
ggsave(filename = "penguin-plot.png")

• Or you can save the plot object and save that

p <- penguins |> 
    ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
    geom_point()
ggsave(filename = "penguin-plot.png", p)

Exploring the diamonds data set

Diamonds data set

Consider the diamonds dataset in ggplot2

• Contains the prices and other attributes of almost 54,000 diamonds.

diamonds

# A tibble: 53,940 × 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1  0.23 Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
 2  0.21 Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
 3  0.23 Good      E     VS1      56.9    65   327  4.05  4.07  2.31
 4  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
 5  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
 6  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
 7  0.24 Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
 8  0.26 Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
 9  0.22 Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
10  0.23 Very Good H     VS1      59.4    61   338  4     4.05  2.39
# ℹ 53,930 more rows

Geometric objects

How are these two plots similar?

ggplot(diamonds, aes(carat, price)) + 
  geom_point() + 
  theme(axis.title = element_text(size=28), 
        axis.text = element_text(size=20))

ggplot(diamonds, aes(carat, price)) + 
  geom_smooth() + 
  theme(axis.title = element_text(size=28), 
        axis.text = element_text(size=20))

• Both plots contain the same x and y variables; both plots describe same data.
• Each plot uses a different geometric object, geom, to represent the data.

Geometric objects

• Can utilize multiple geoms together to elucidate relationship

ggplot(diamonds, aes(carat, price)) + 
  geom_point() + 
  geom_smooth()

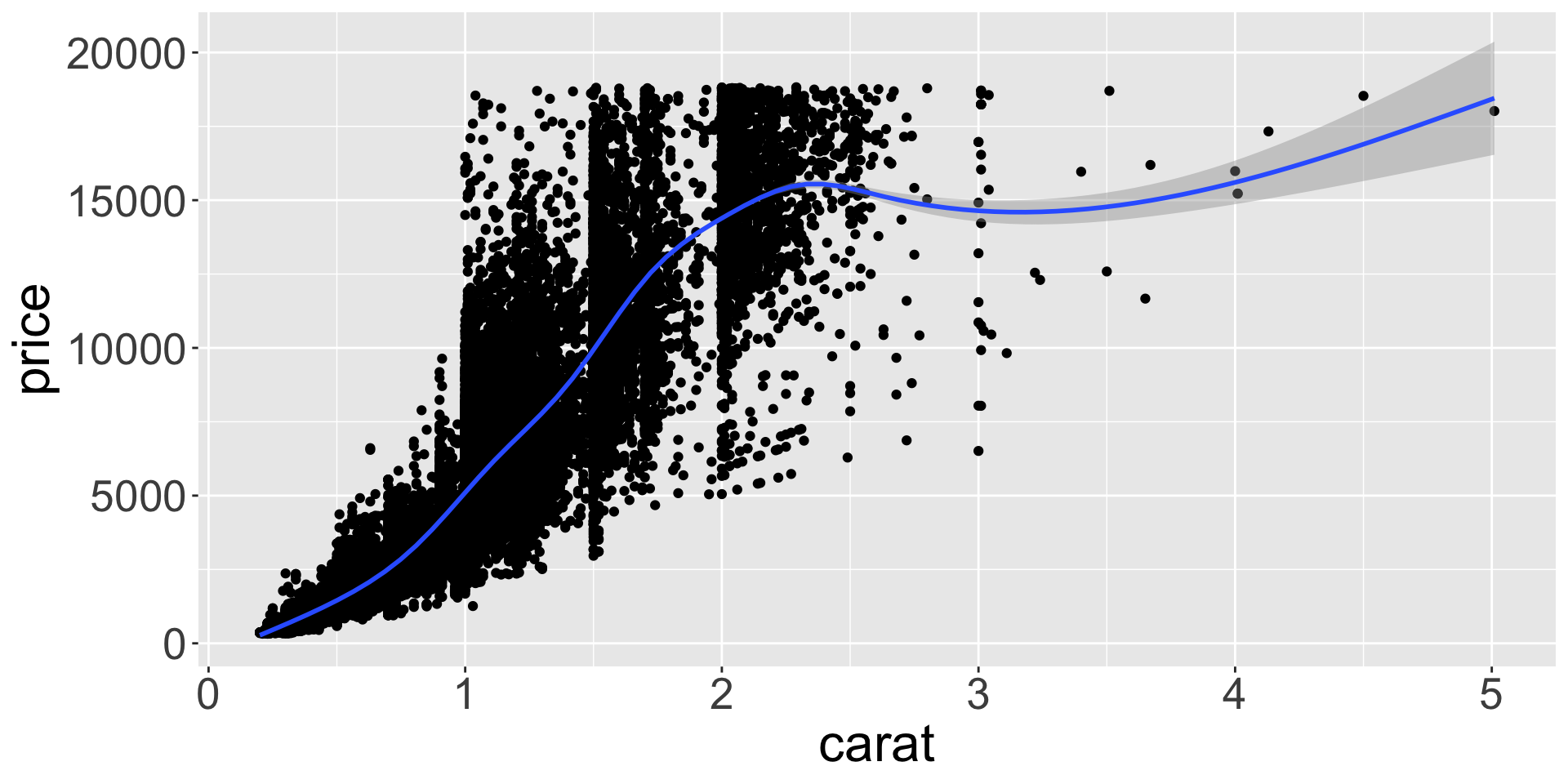
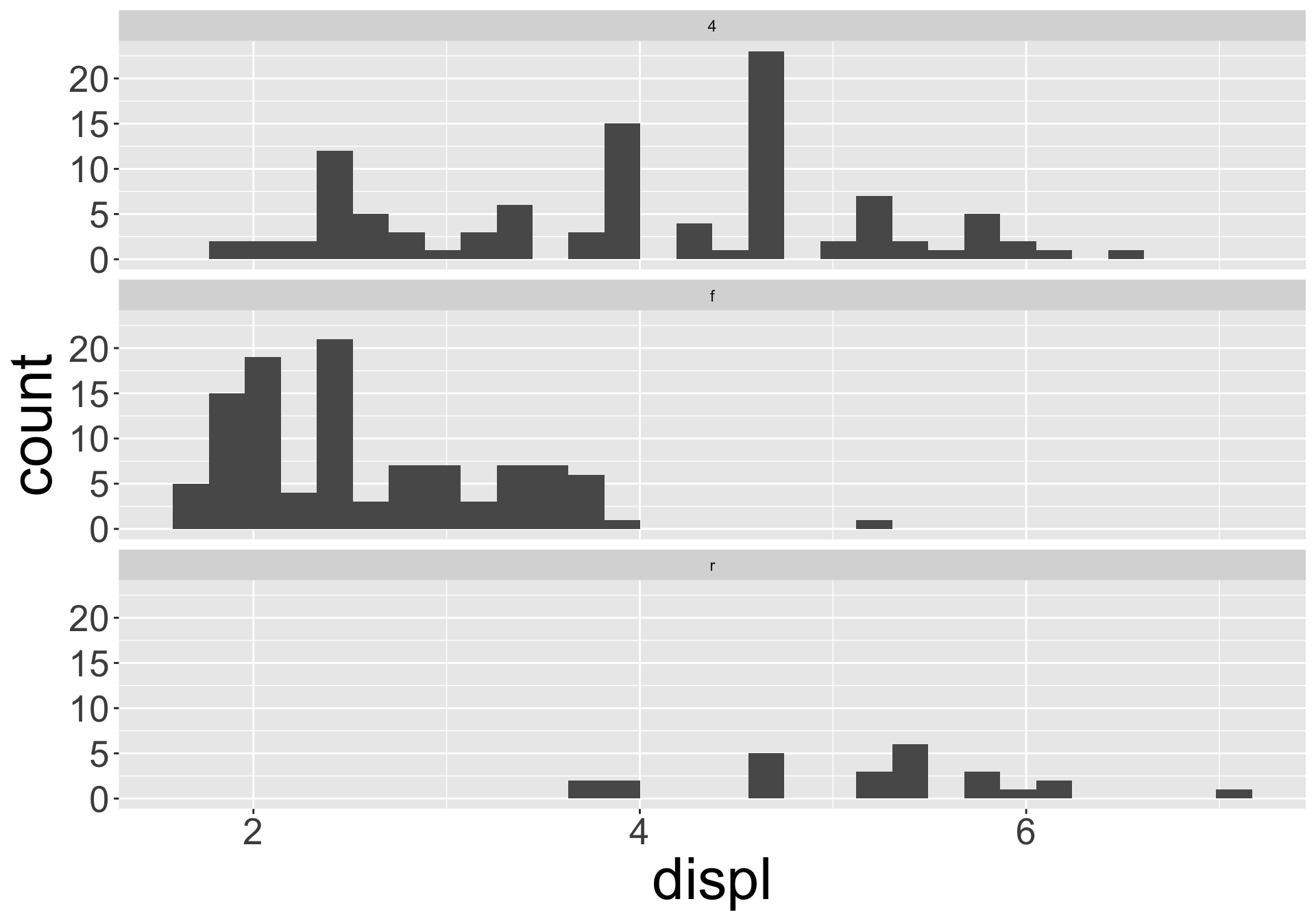
Statistical transformations

Let’s create a bar chart across cuts:

ggplot(diamonds, aes(x = cut)) +
  geom_bar()

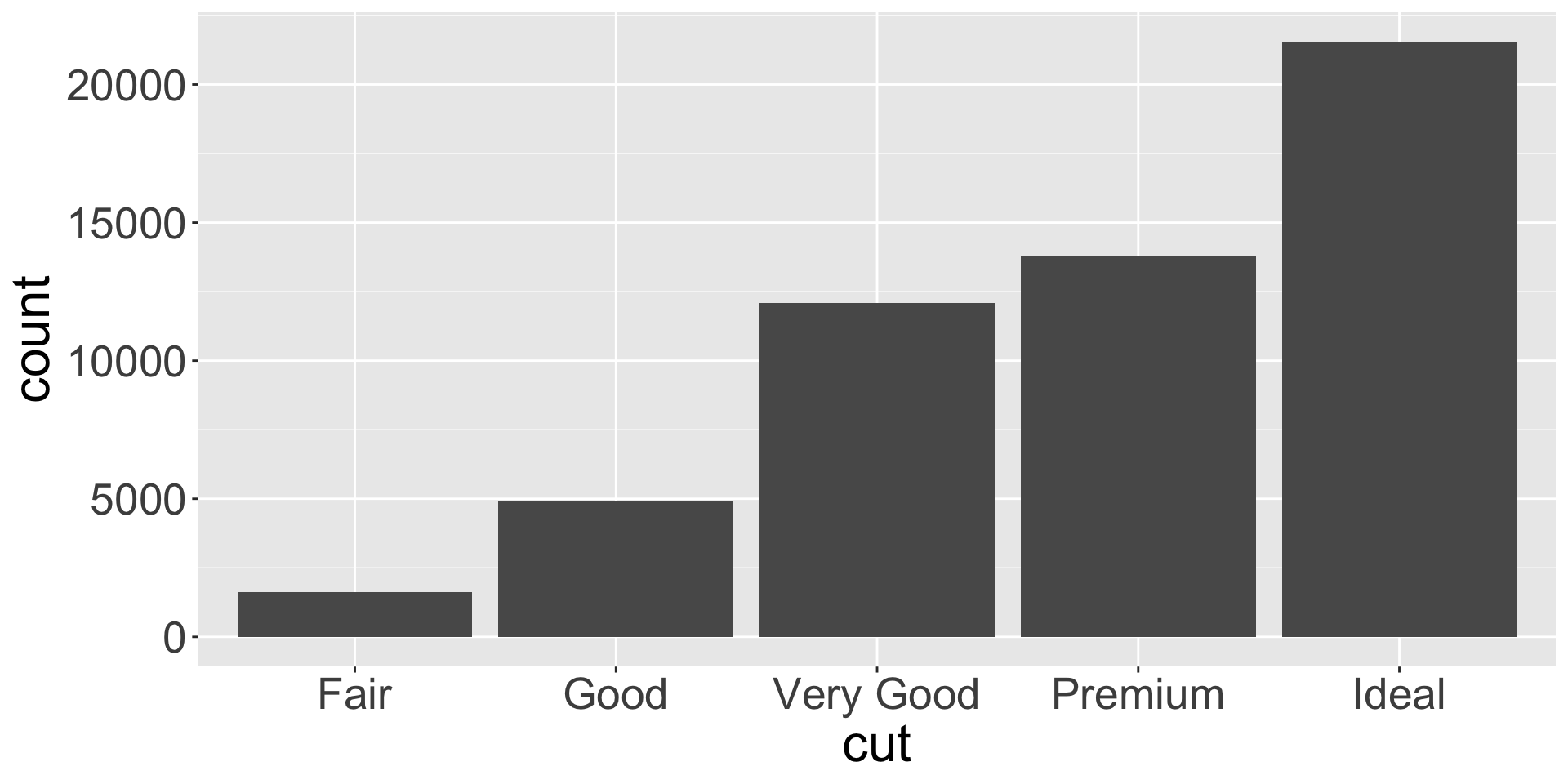
• count is not a variable in diamonds, so how is it creating this?

Statistical transformations

Examples

• Bar charts, histograms, and frequency polygons bin your data, then plot bin counts (the number of points that fall in each bin).
• Smoothers fit a model to your data and then plot predictions from the model.
• Boxplots compute the five-number summary of the distribution and then display that summary as a specially formatted box.

Statistical transformations

The algorithm used to calculate new values for a graph is called a stat.

• (stat is short for statistical transformation)

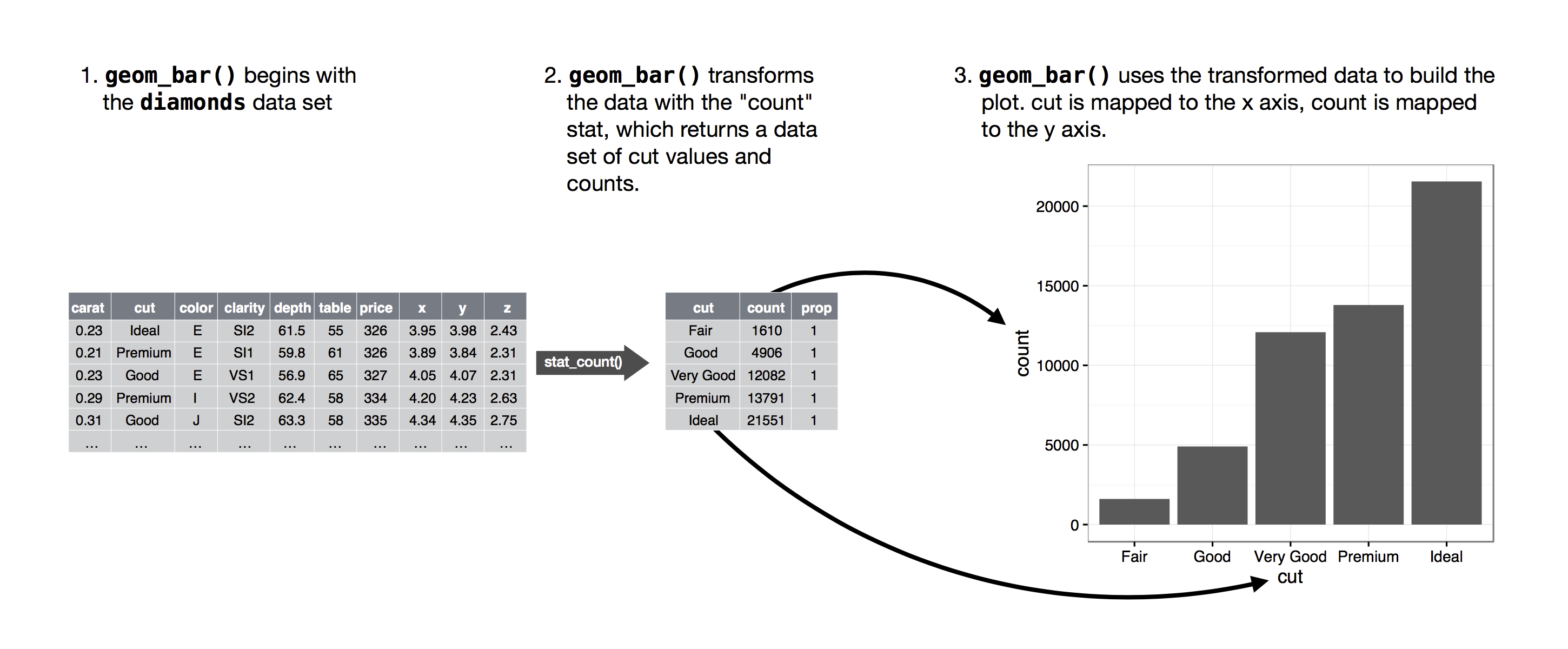
Figure 2

Exploring variables

Two question categories:

1. What type of variation occurs within each variable?
   
2. What type of covariation occurs between 2+ variables?

Variation

Variation is tendency for values of a variable to change from measurement to measurement

• Can be due to measurement error (e.g., measuring height with different rulers) or due to within-group variation (different people have different heights)
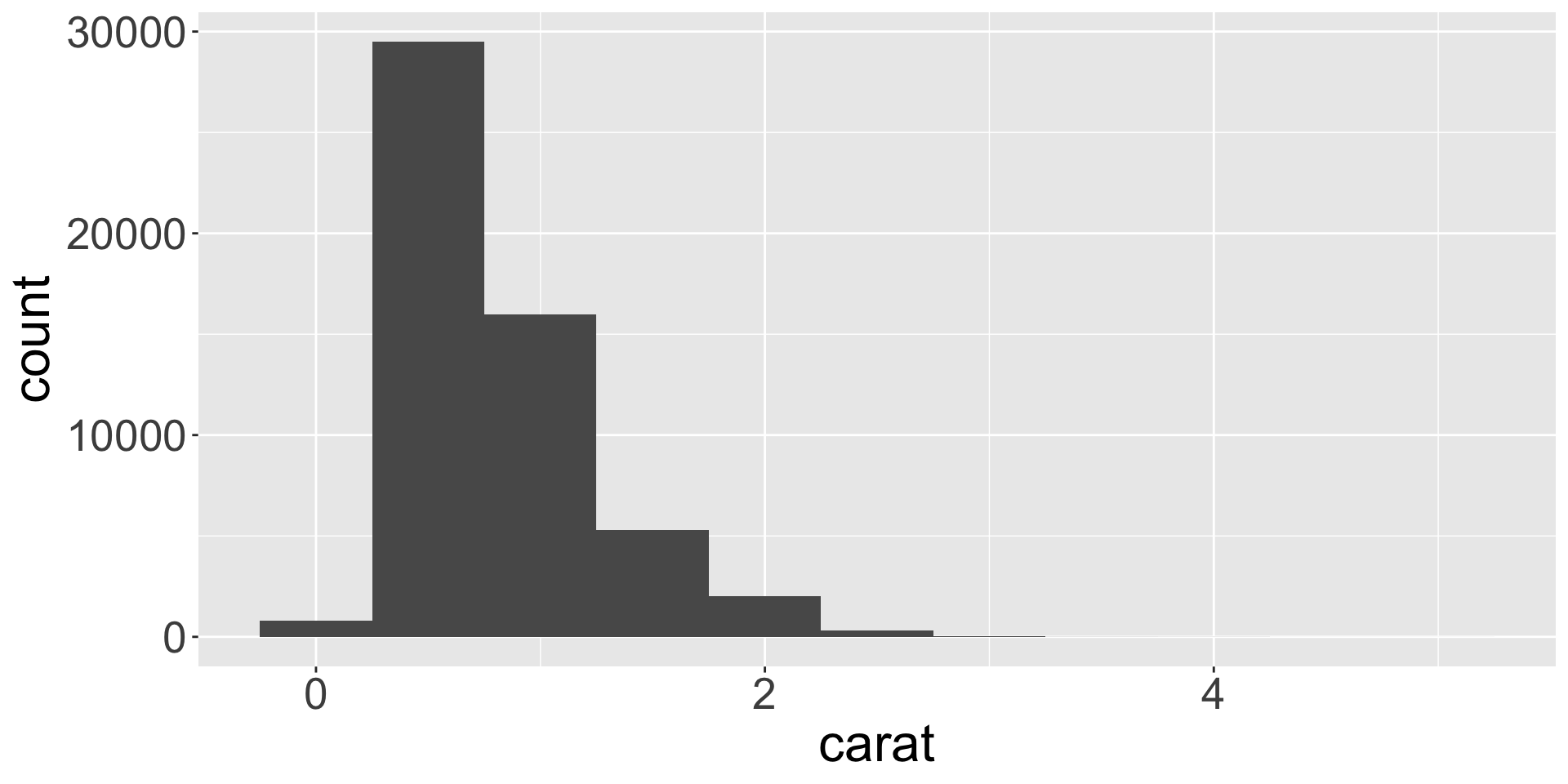
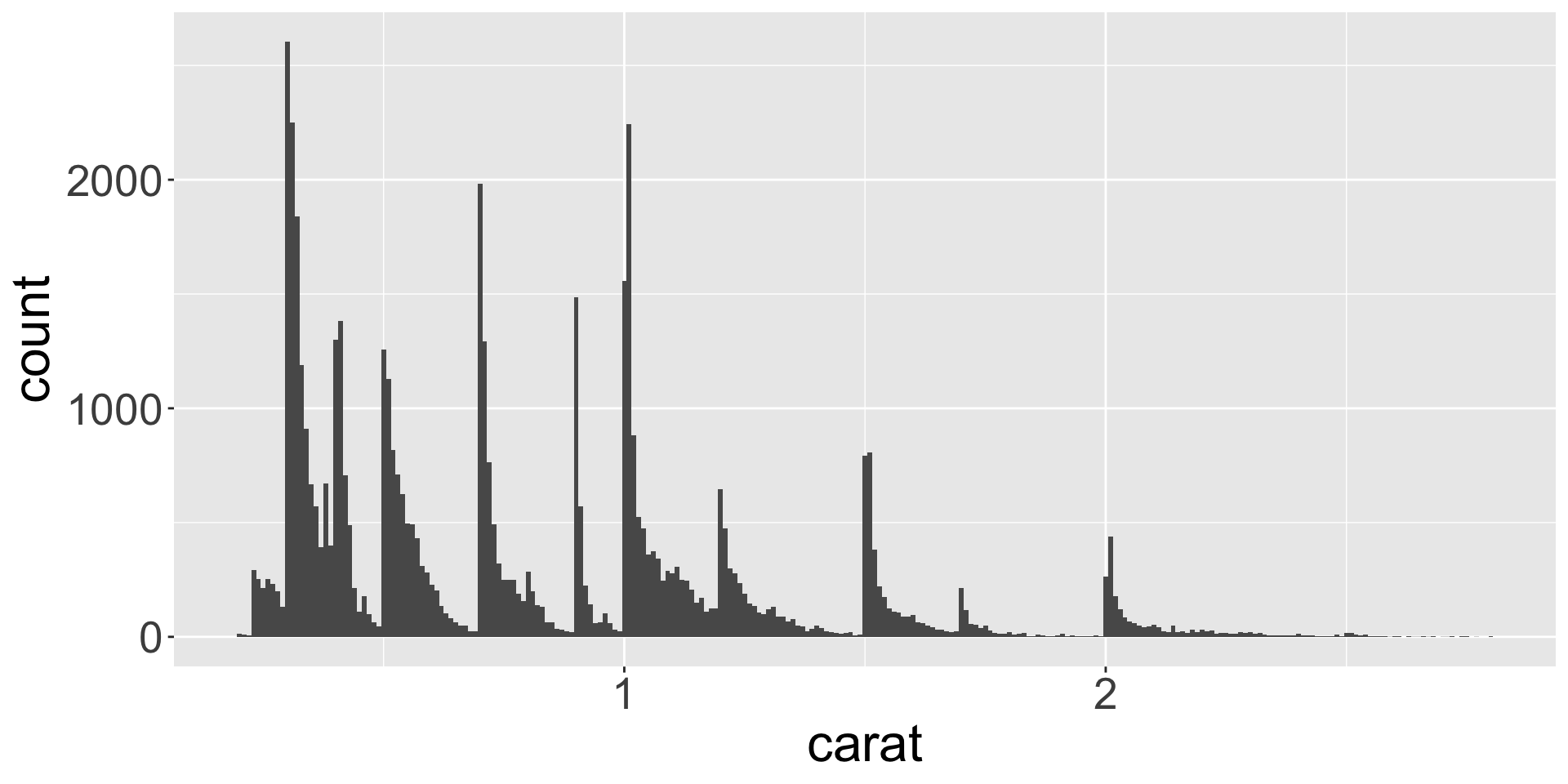
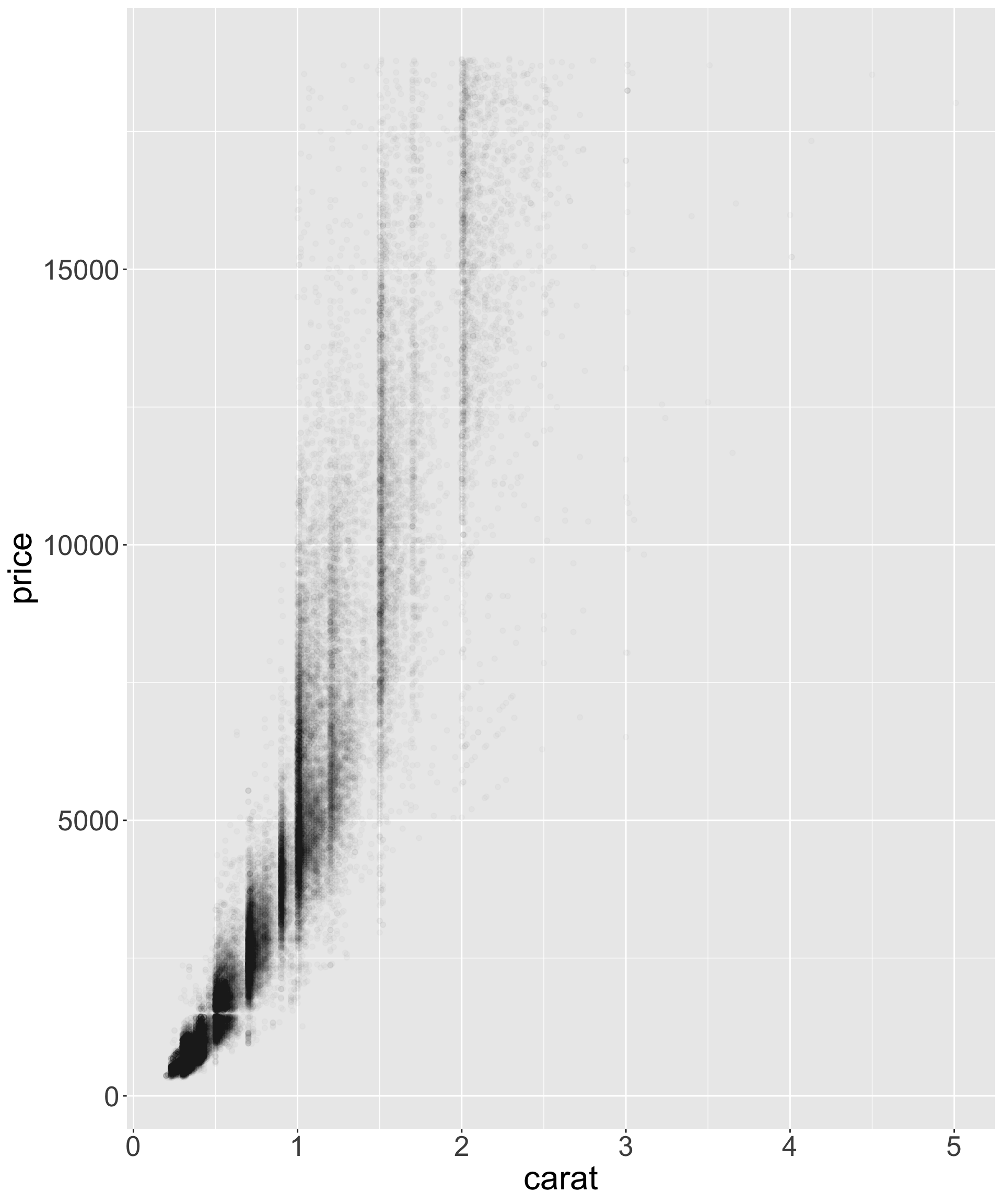
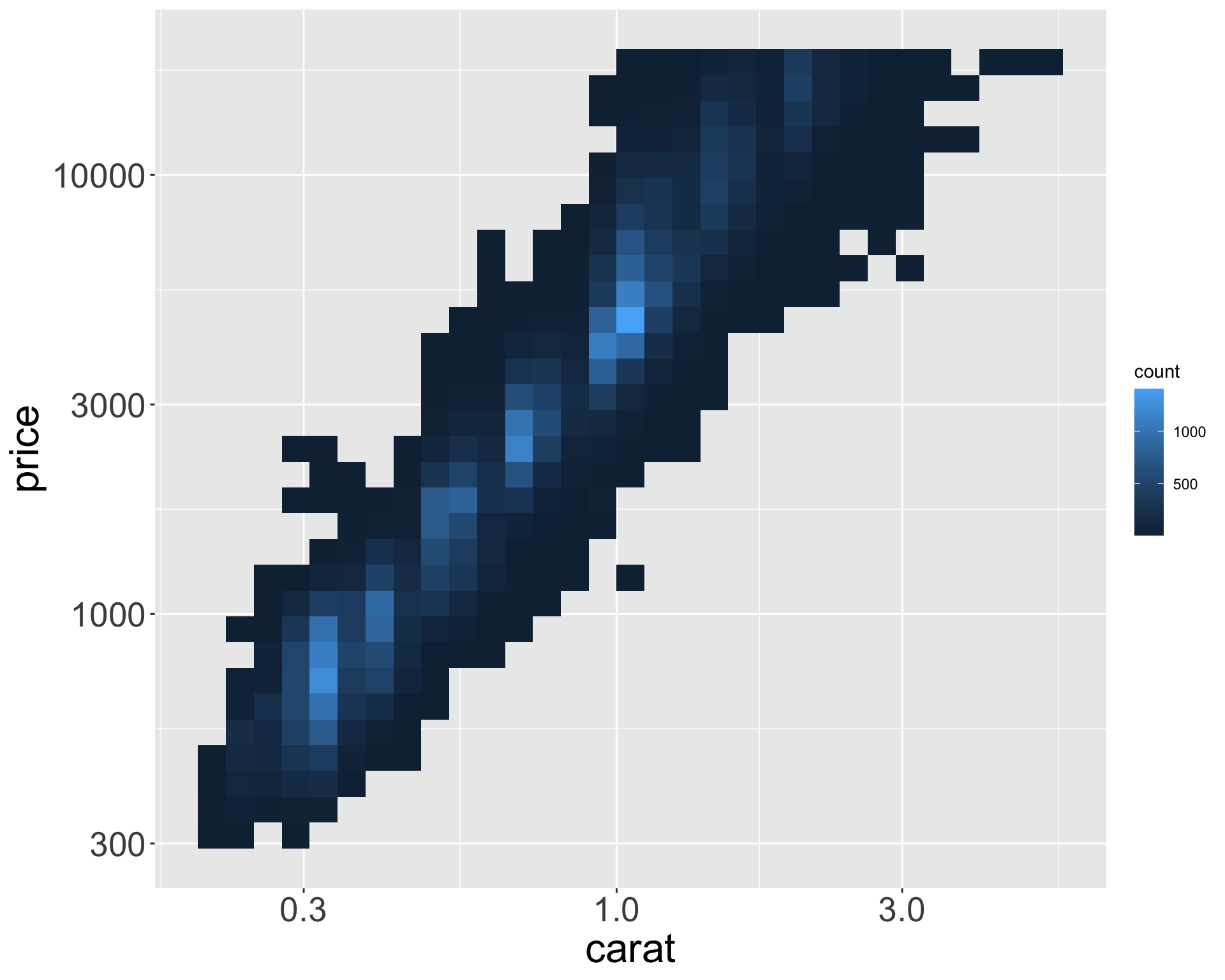
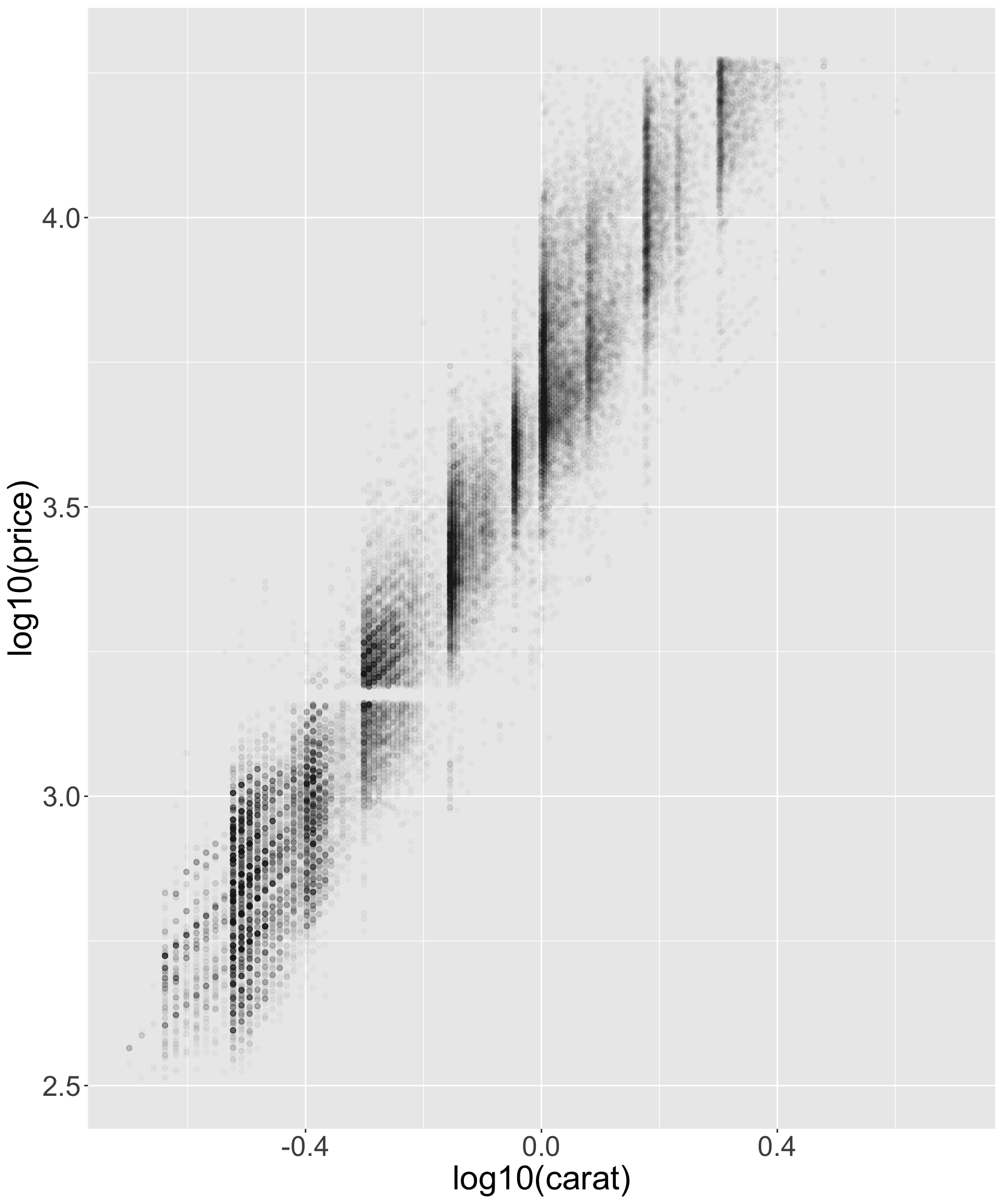
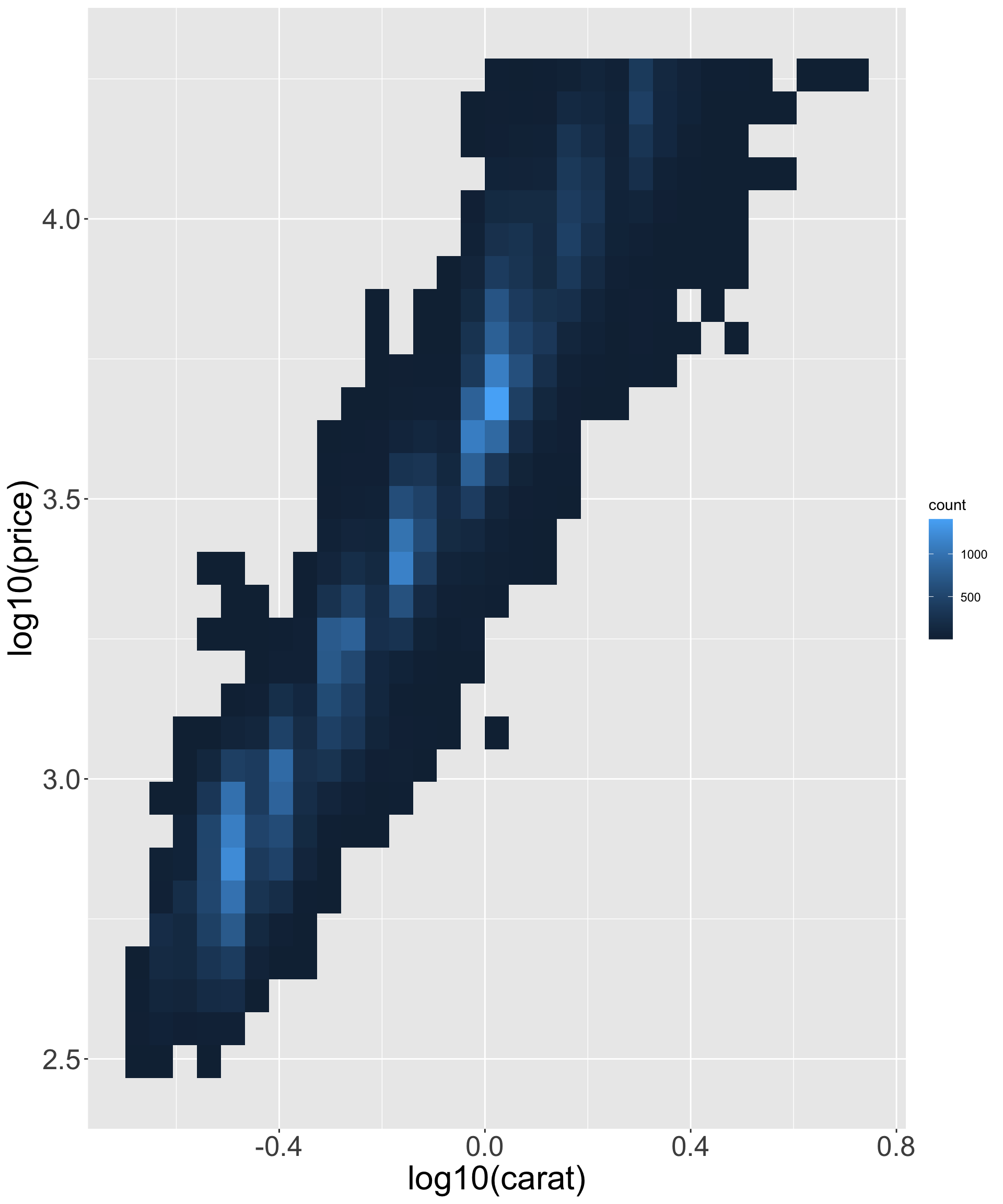
• Let’s explore the distribution of weights (carat) of the ~50k diamonds from diamonds dataset.
• carat is numerical, can use histogram:

diamonds |>
    ggplot(aes(x = carat)) +
    geom_histogram(binwidth = 0.5)

Typical values

• In bar charts and histograms, tall bars = common values; no bars = values not seen
• Questions to ask yourself:
  • Which values are the most common? Why?
  • Which values are rare? Why? Does that match your expectations?
  • Can you see any unusual patterns? What might explain them?
• Let’s look at distribution of weights of smaller diamonds.

diamonds |> 
  filter(carat < 3) |> 
  ggplot(aes(x = carat)) +
  geom_histogram(binwidth = 0.01)

• Why are there more diamonds at whole carats than fractional?
• Why are more diamonds slightly to the right of each peak than slightly to left?

Unusual values

If you encounter unusual values in dataset, and want to ignore them for rest of analysis, two options:

1. Drop entire row with the strange values, e.g.

diamonds_filtered <- diamonds |>
  filter(between( y, 3, 20))

2. Replacing unusual values with missing values

diamonds2 <- diamonds |>
  mutate(y = if_else(y < 3 | y > 20, NA, y))

• Latter is more recommended behavior.

Covariation

… is tendency for values of 2+ variables to vary together in a related way

• How does price (numerical) of a diamond vary with quality (categorical)?
• Can use geom_freqpoly() to show “frequency polygons” (similar to histogram)

ggplot(diamonds, aes(x = price)) +
  geom_freqpoly(aes(color = cut), binwidth = 500, linewidth = 0.75)

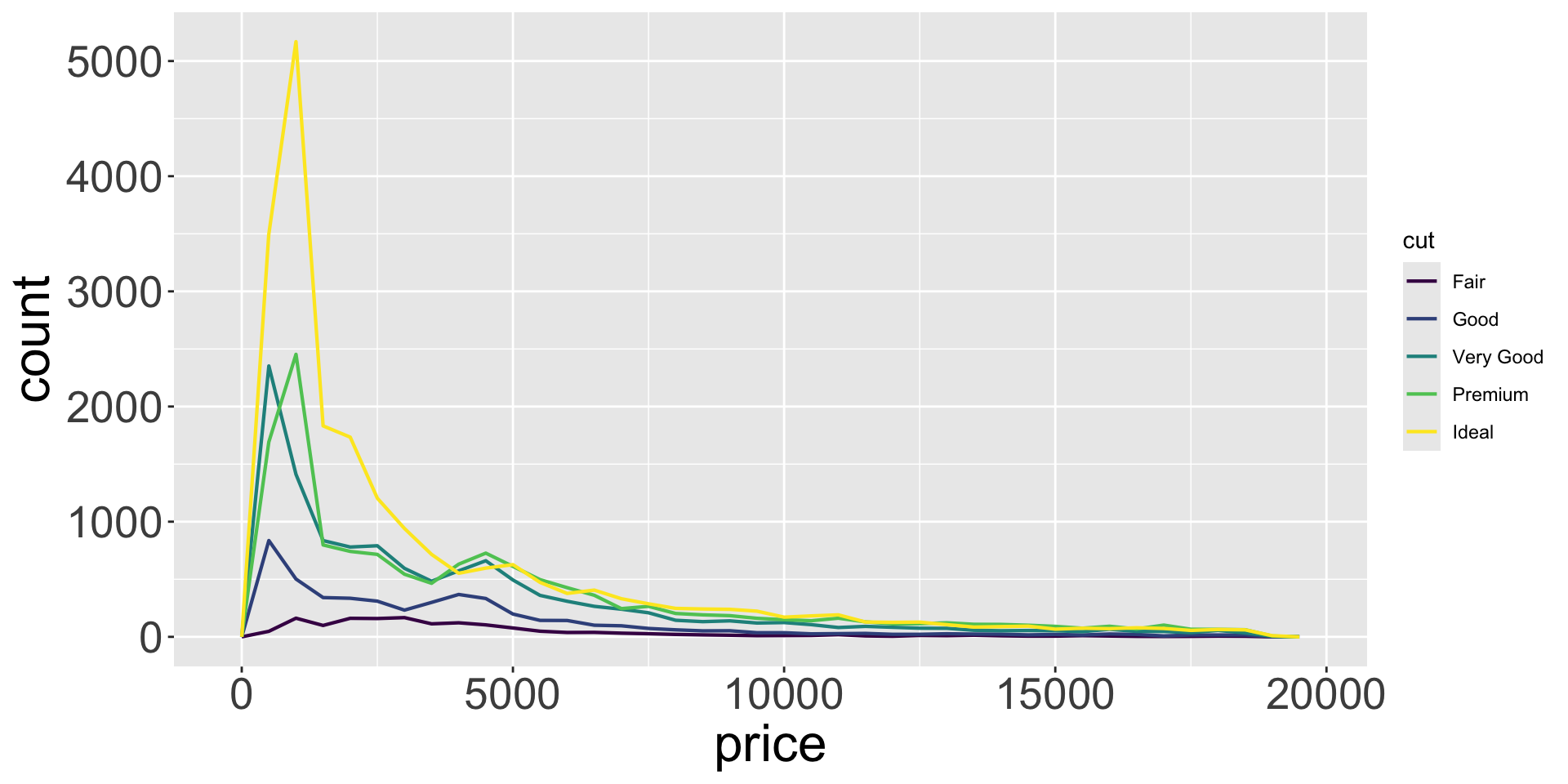
• Not super informative, since the height mainly reflects the count.

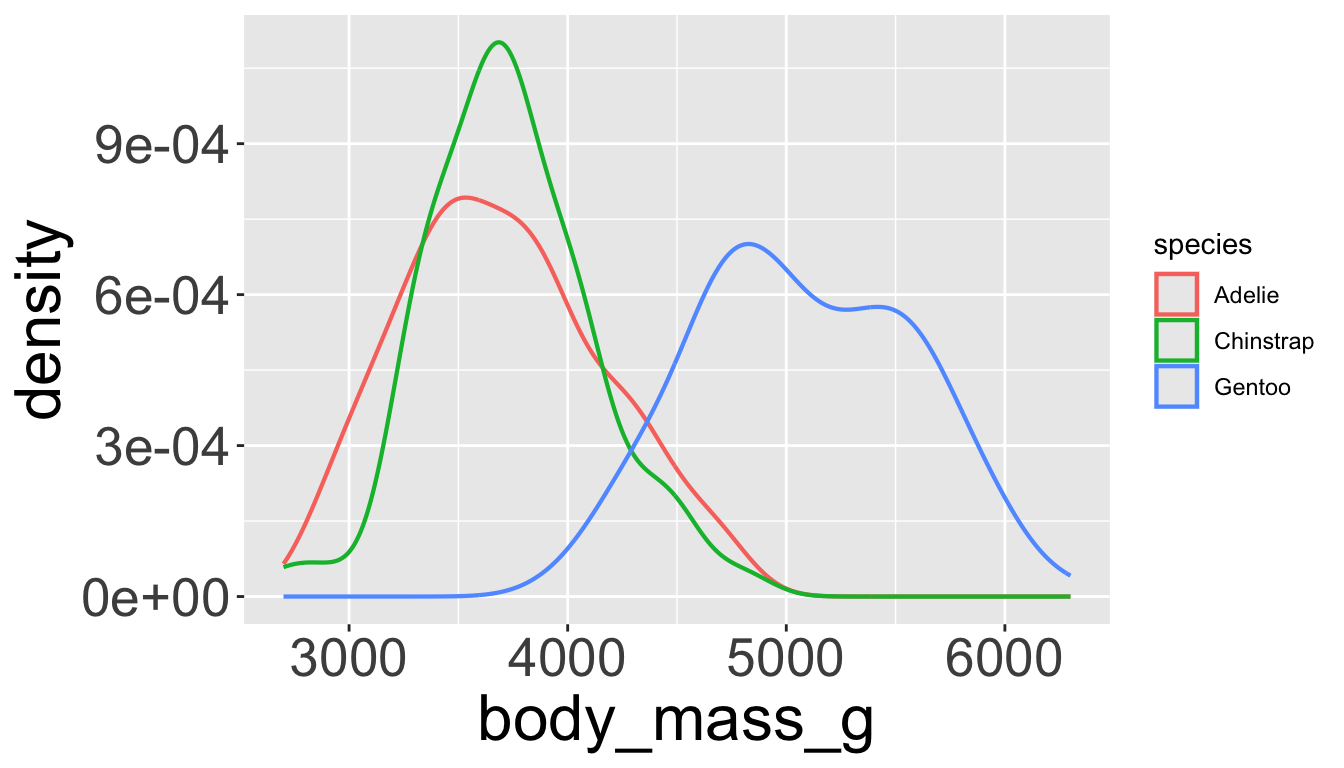
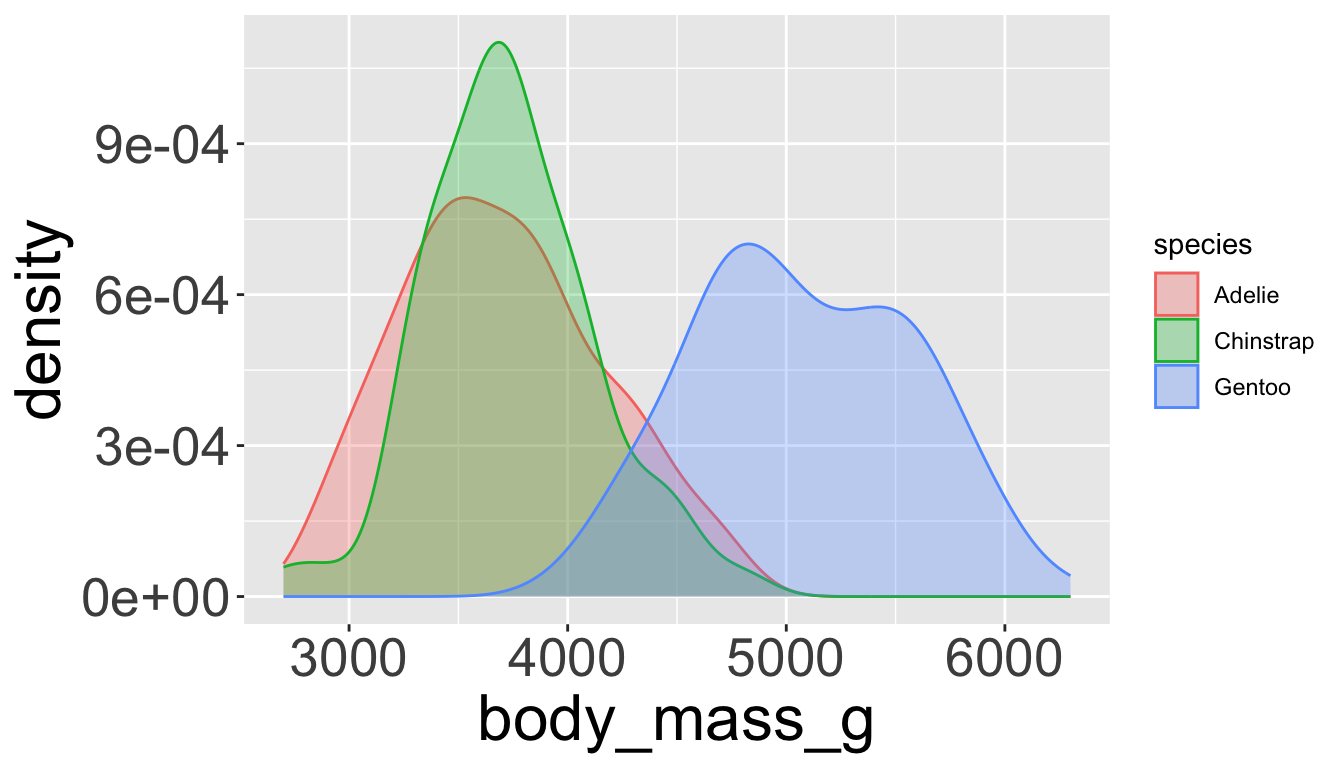
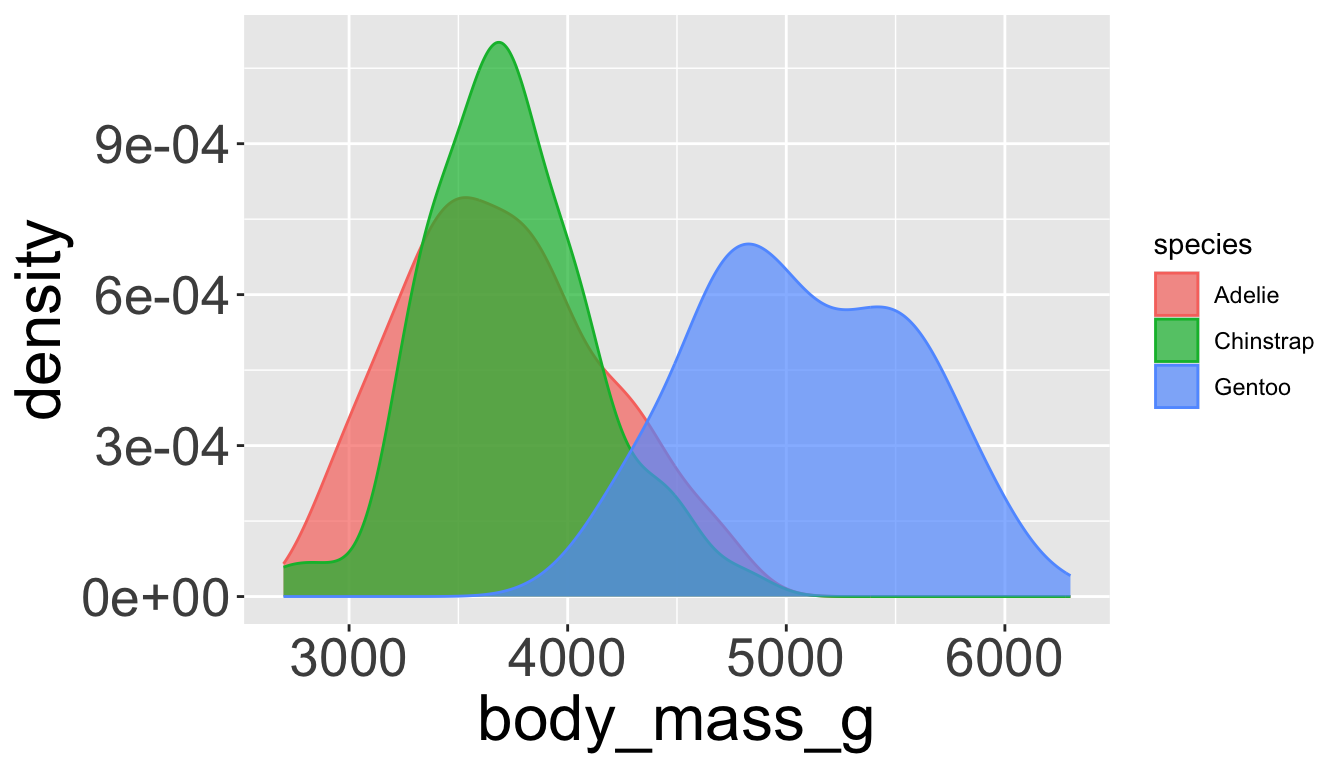
Covariation

• More useful to understand the density of the variable (count / total number)
• To do this, we can use after_stat(density), which does this normalization

ggplot(diamonds, aes(x = price, y = after_stat(density))) +
  geom_freqpoly(aes(color = cut), binwidth = 500, linewidth = 0.75)

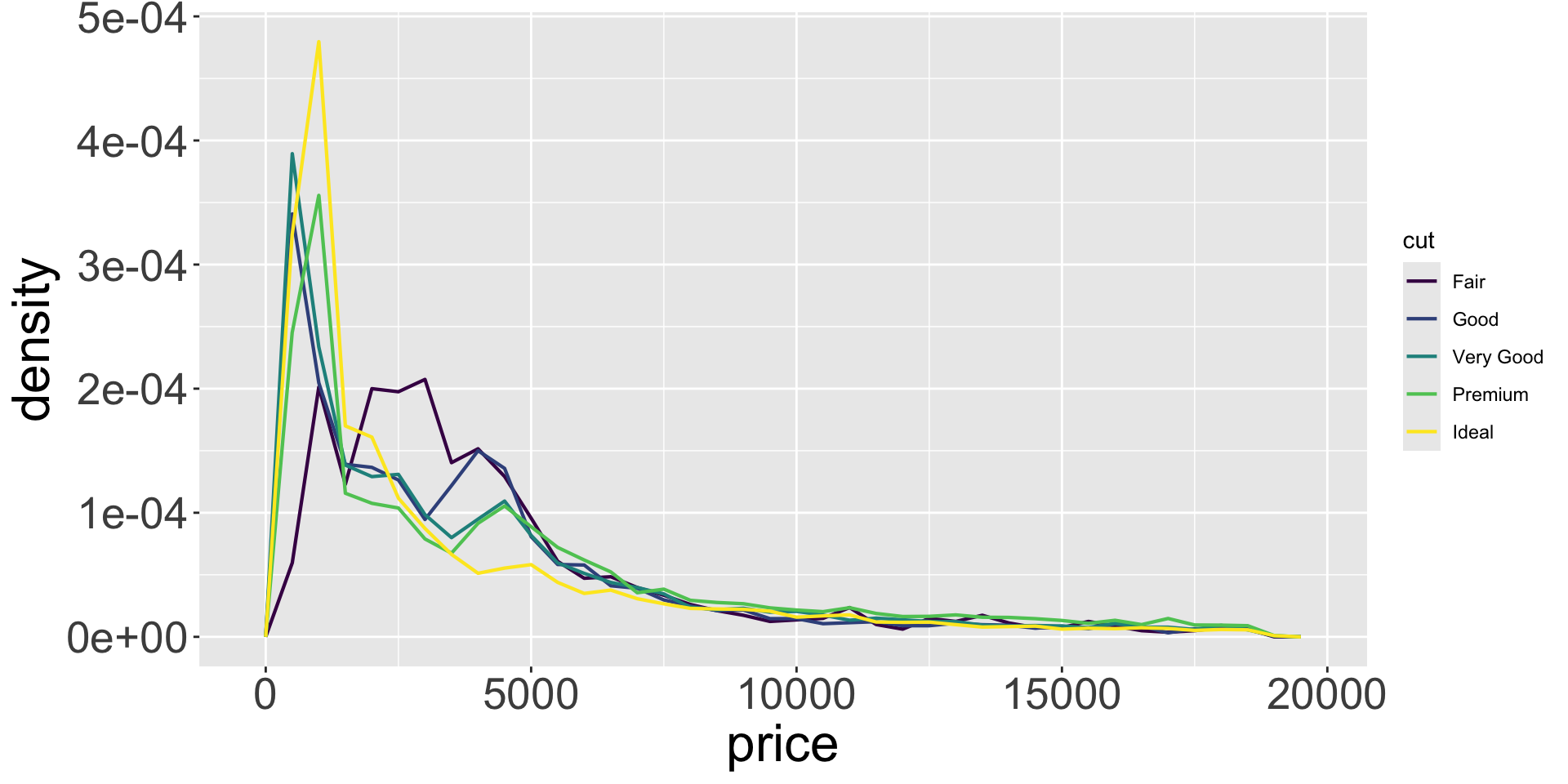
• Seems diamond quality has no significant effect?

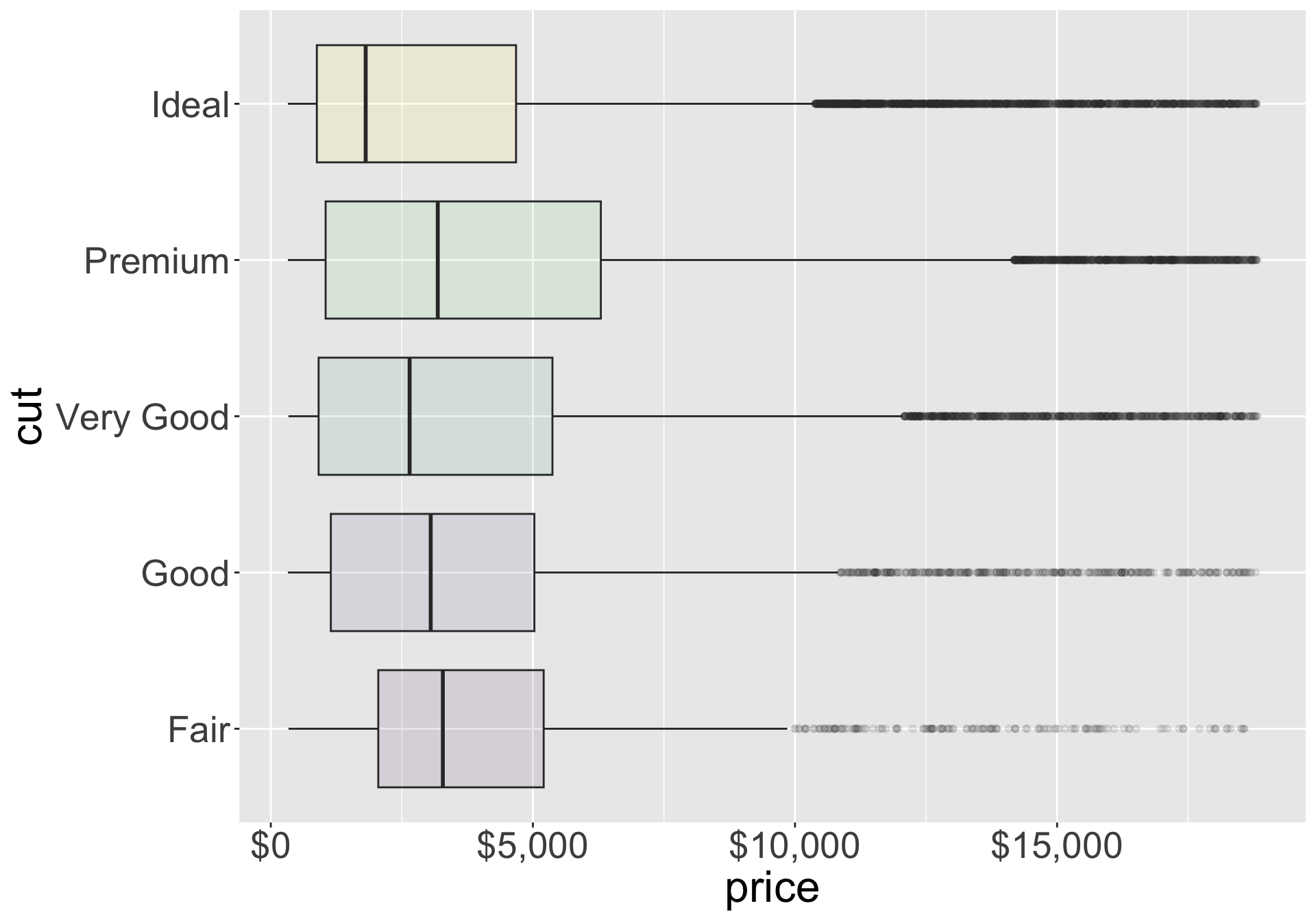
Covariation

• Let’s further inspect with a box plot

ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
  geom_boxplot()

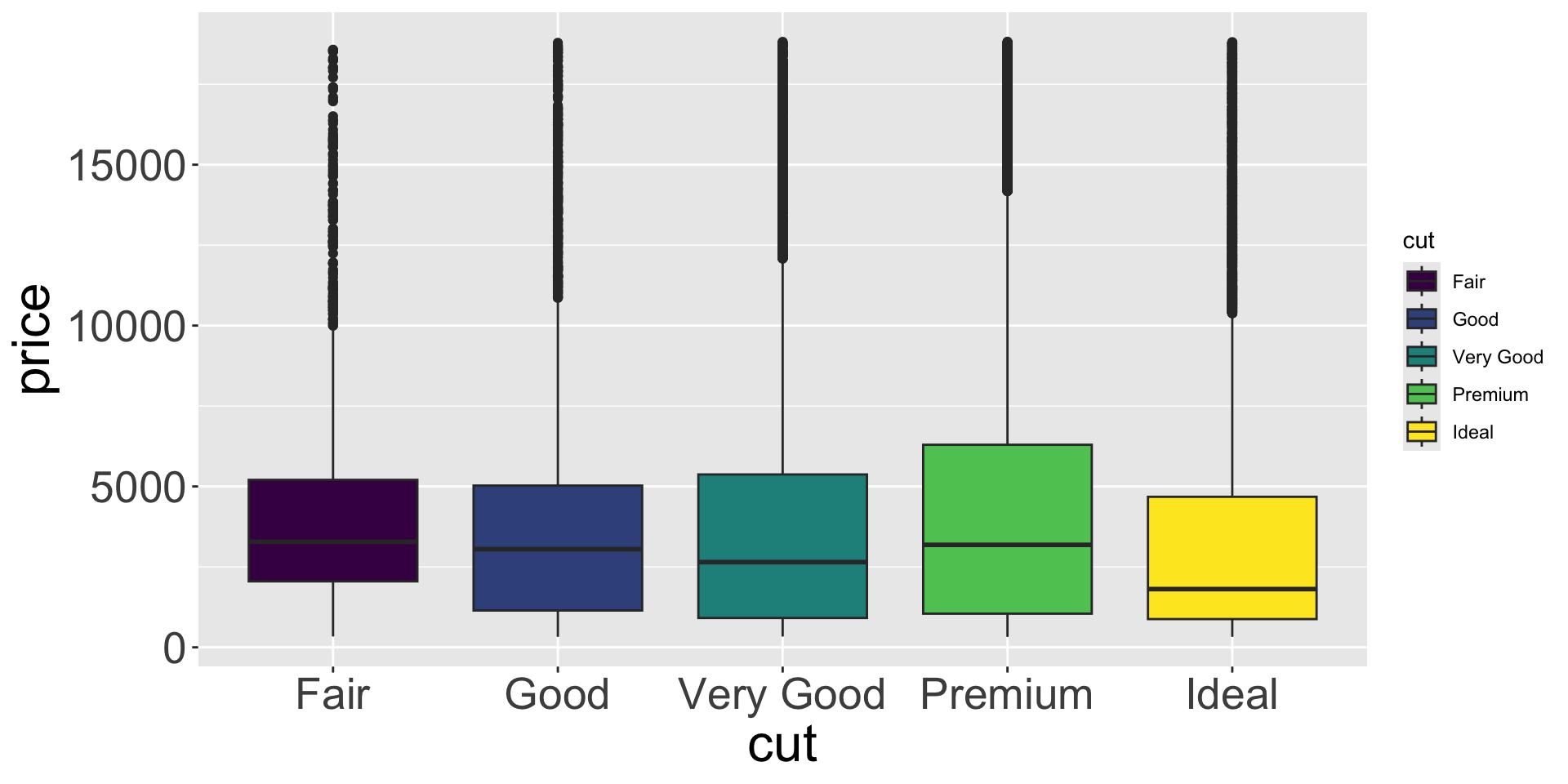
• Can now easily compare medians and 25th/75th percentiles
• Better quality diamonds are typically cheaper?! We’ll investigate why.

Better quality diamonds are typically cheaper?!

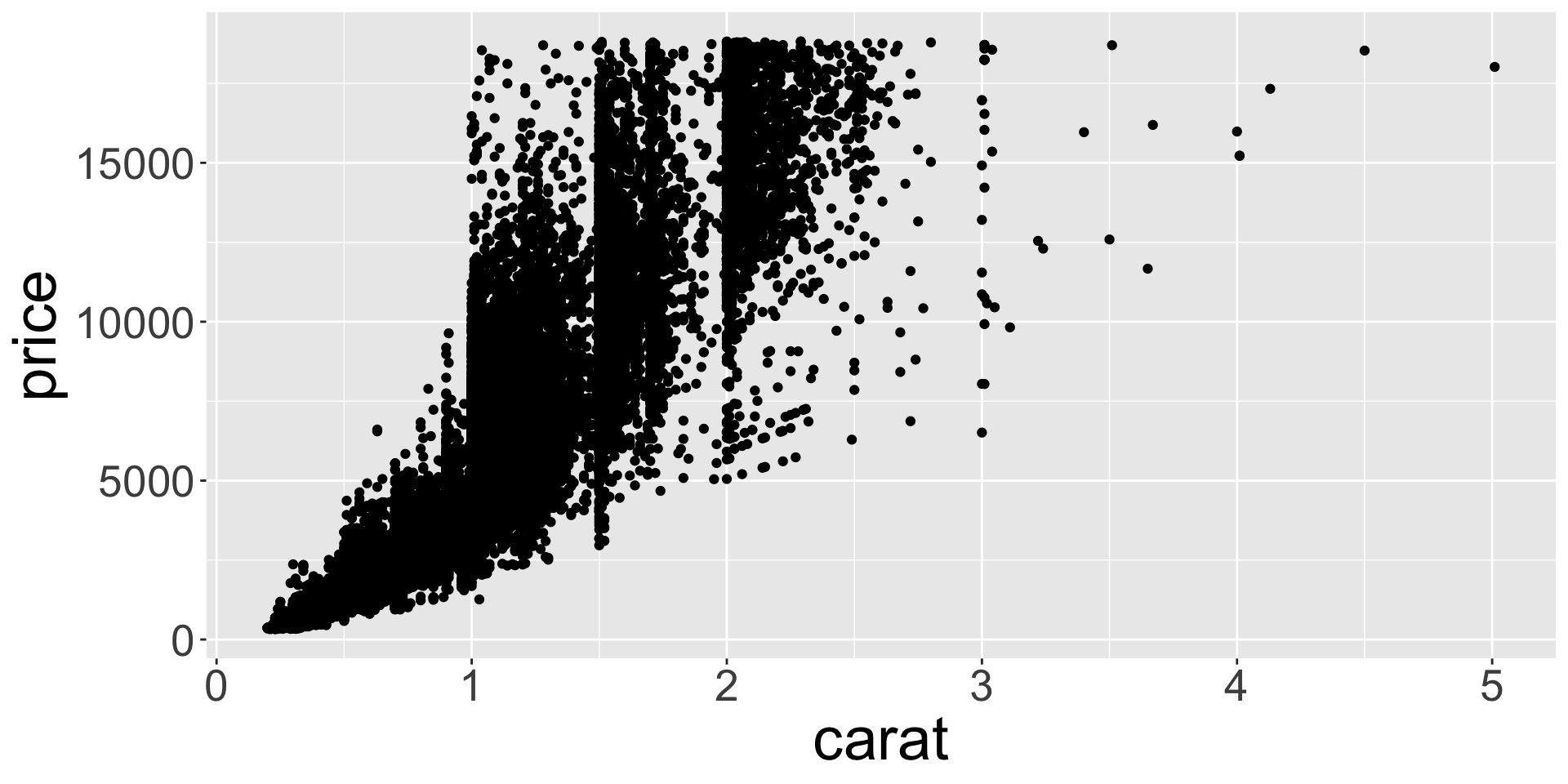
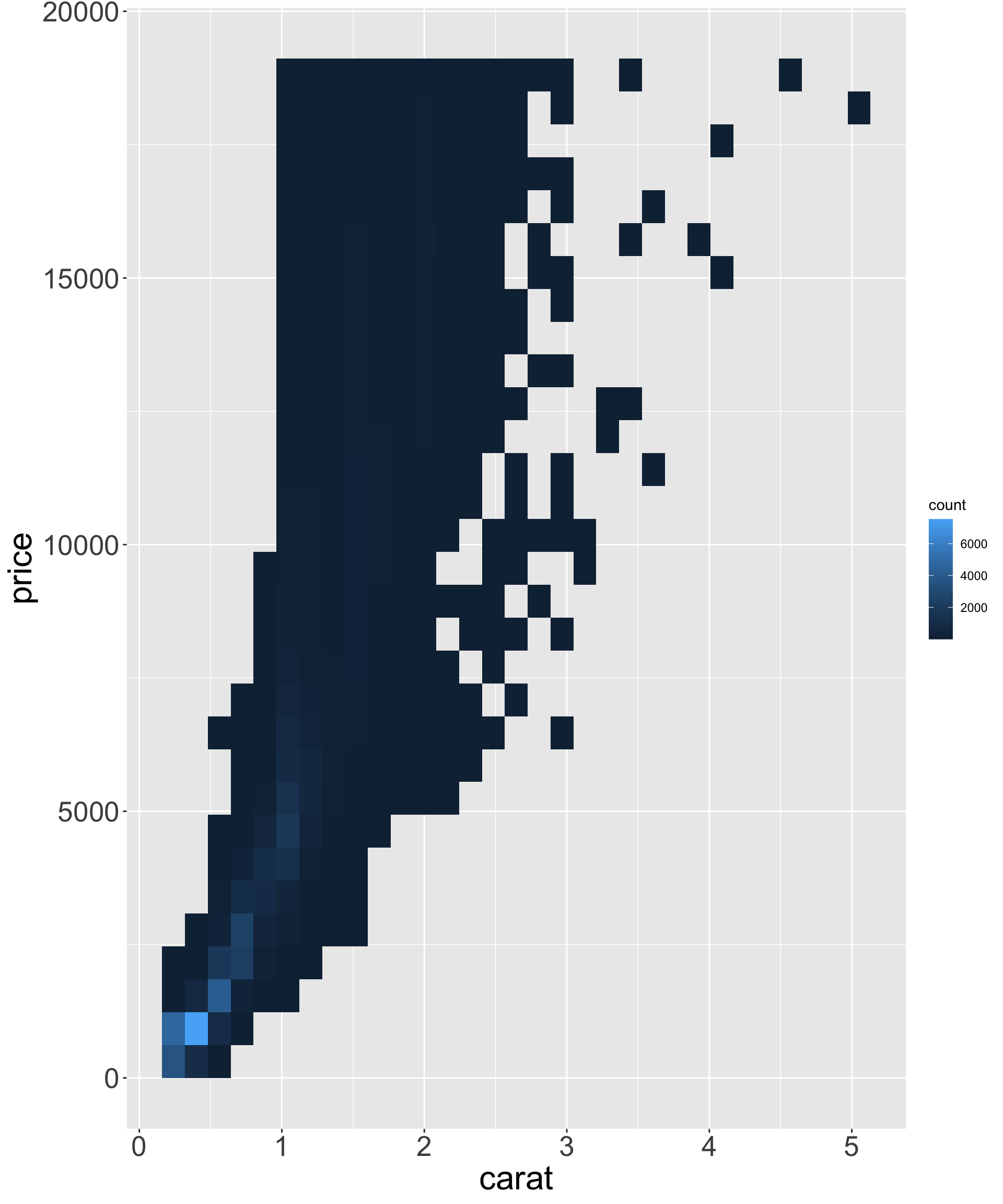
• What might be responsible for this? Recall variables: x,y,z refer to length/width/depth of diamond in mm

colnames(diamonds)

 [1] "carat"   "cut"     "color"   "clarity" "depth"   "table"   "price"  
 [8] "x"       "y"       "z"      

• Let’s look at size vs price.

Better quality diamonds are typically cheaper?!

ggplot(diamonds, aes(x, price)) + geom_point() + theme(axis.title = element_text(size=40), axis.text = element_text(size=32))
ggplot(diamonds, aes(y, price)) + geom_point() + theme(axis.title = element_text(size=40), axis.text = element_text(size=32))
ggplot(diamonds, aes(z, price)) + geom_point() + theme(axis.title = element_text(size=40), axis.text = element_text(size=32))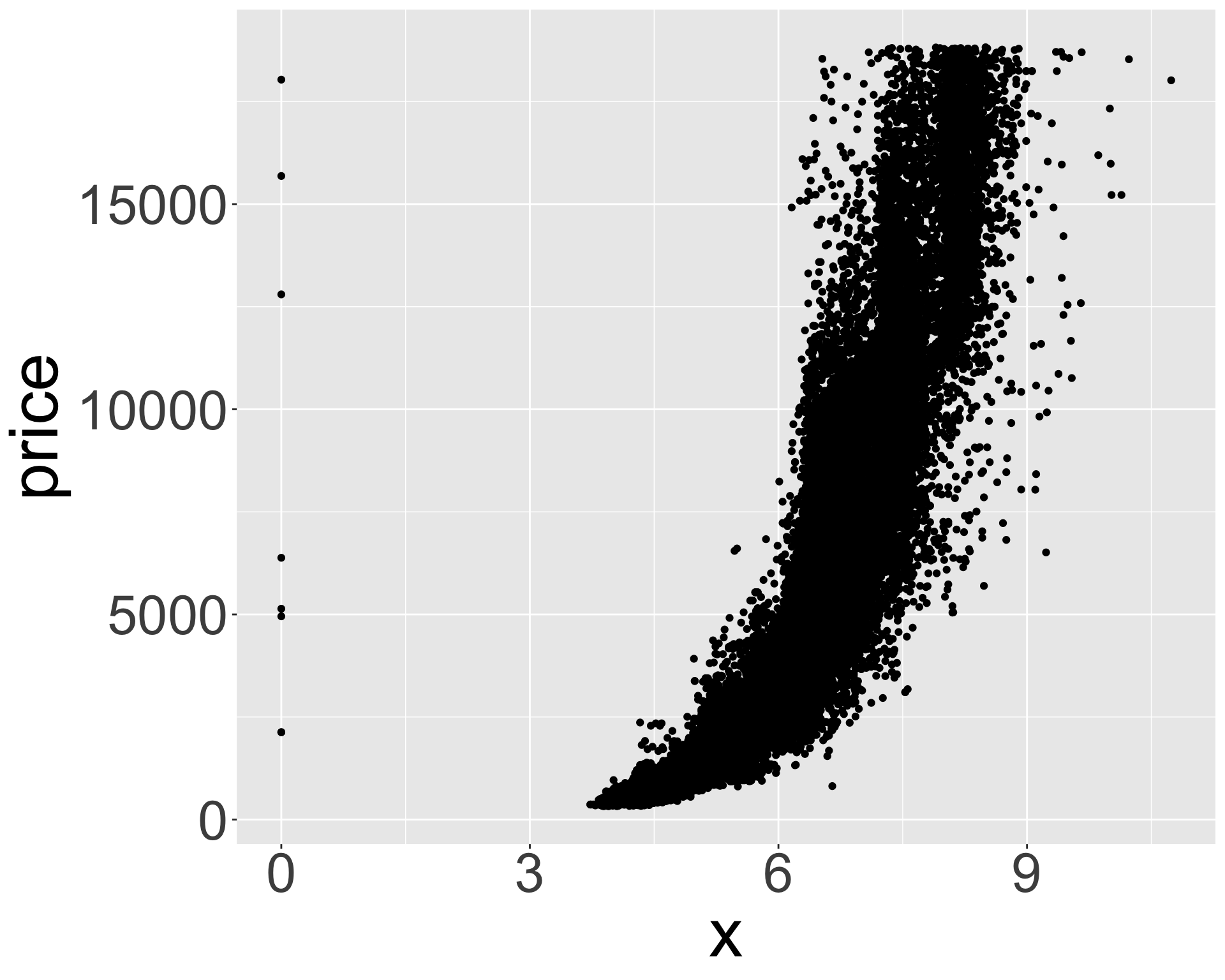

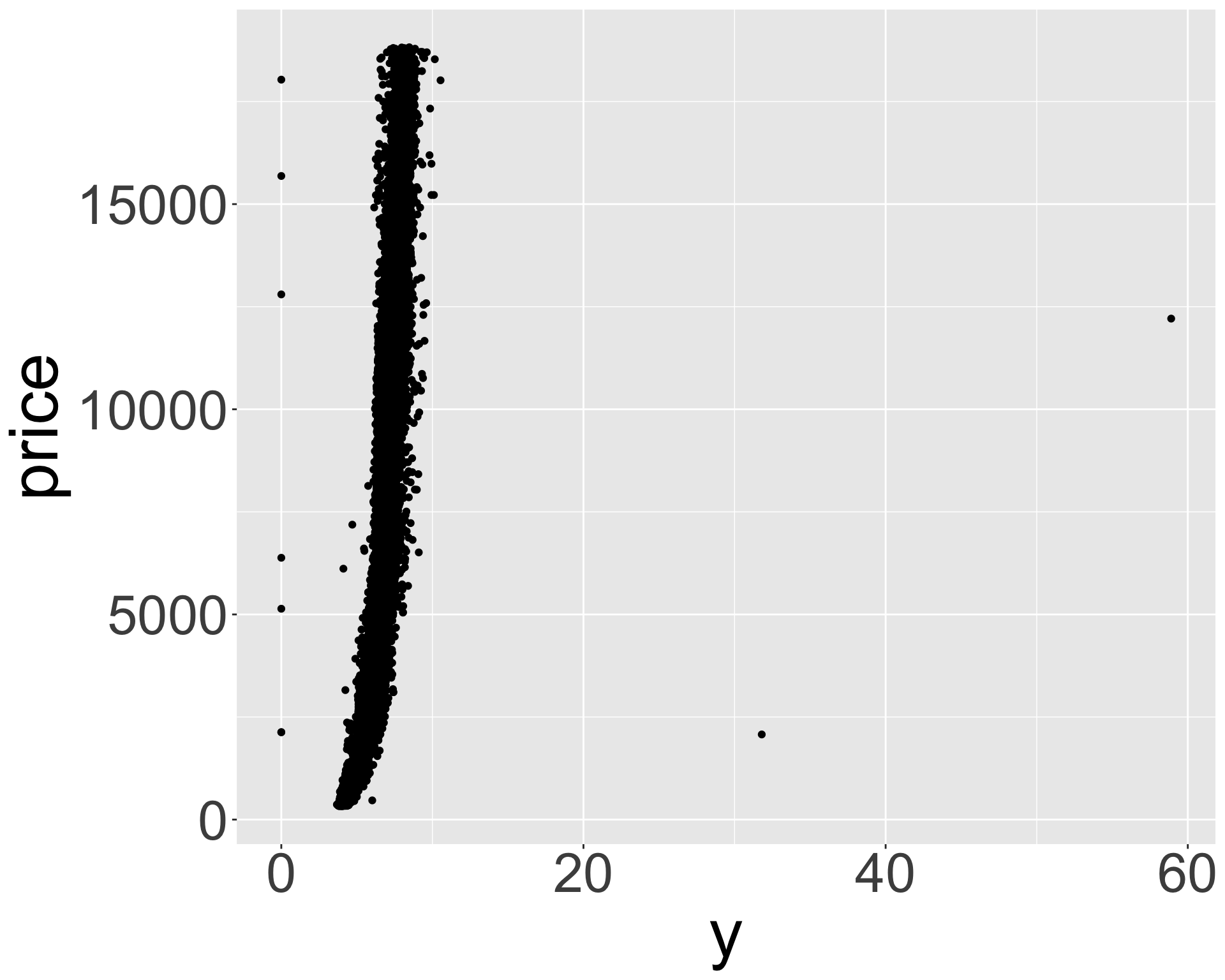
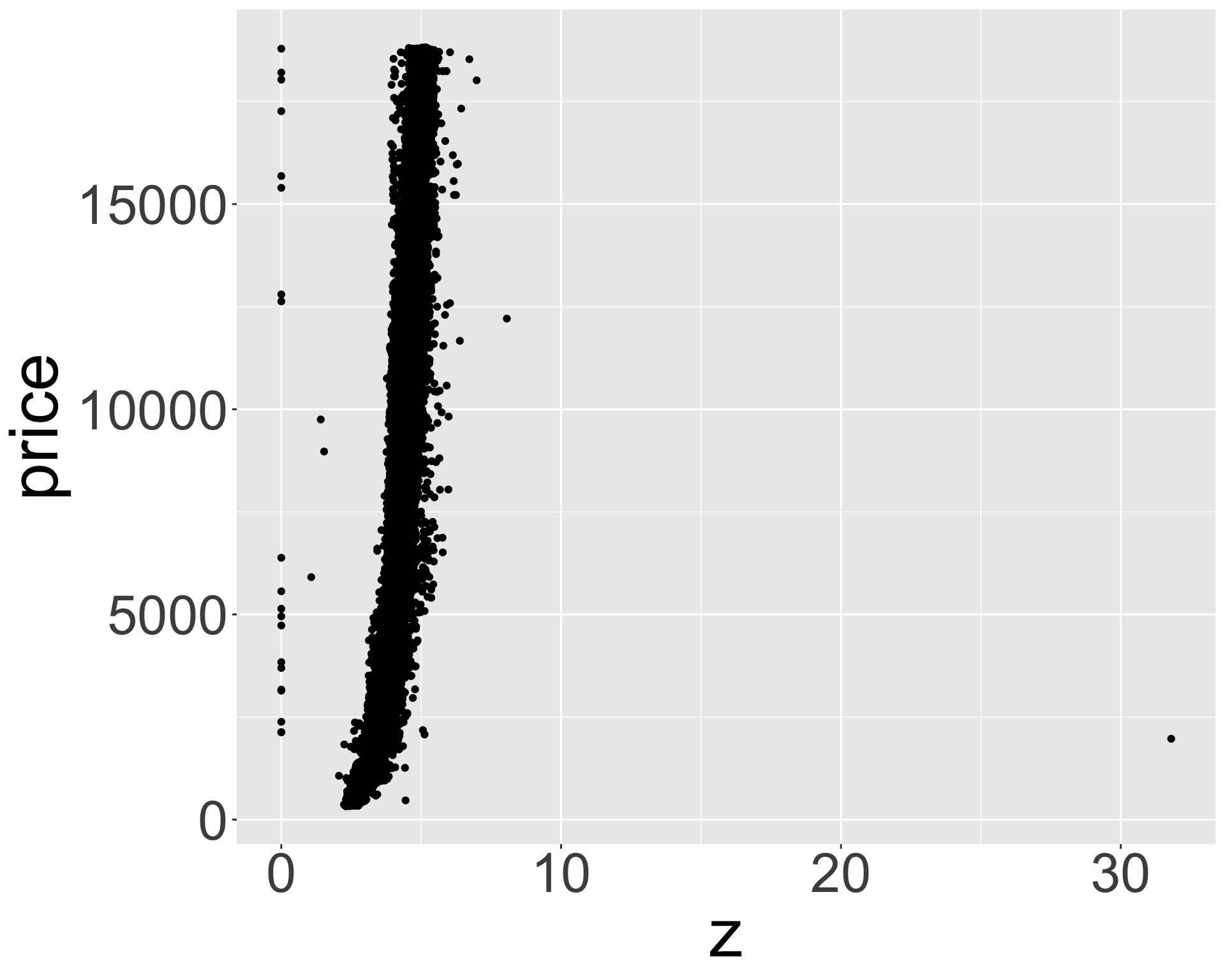
• Clearly some outliers - “zero” length / width / depth diamonds apparently?
• But still some positive correlation between x, y, z and price.
• Let’s clean up the tibble to only view the middle 95% of values for x, y, z.

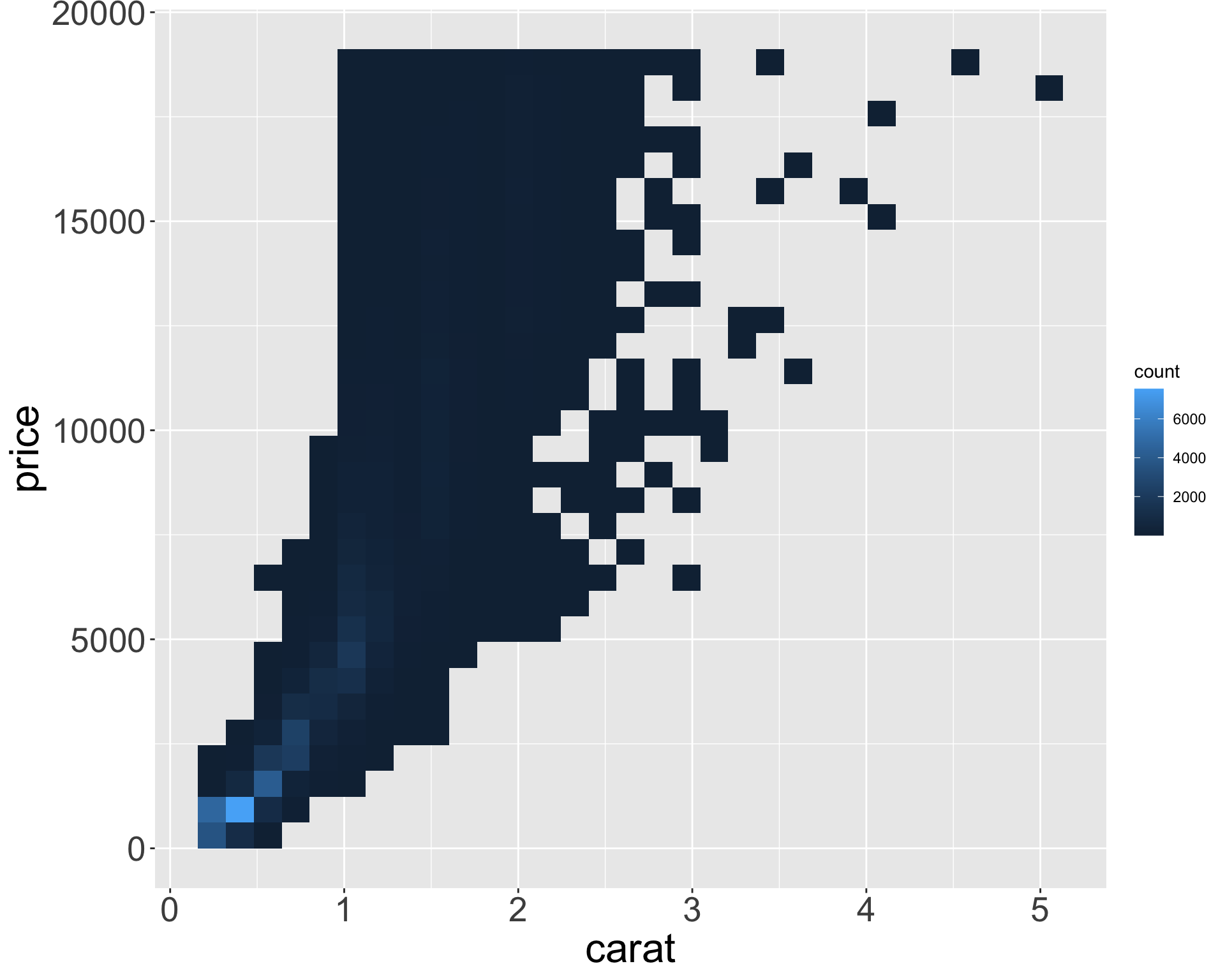
Better quality diamonds are typically cheaper?!

• Let’s clean up the tibble to only view the middle 95% of values for x, y, z

diamonds_middle <- diamonds |> 
  filter(between(x, quantile(x, 0.025), quantile(x, 0.975)),
         between(y, quantile(y, 0.025), quantile(y, 0.975)),
         between(z, quantile(z, 0.025), quantile(z, 0.975)))

or

IsInMiddle95 <- function(a) between(a, quantile(a, 0.025), quantile(a, 0.975))
diamonds_middle_v2 <- diamonds |> 
  filter(if_all(x:z, IsInMiddle95))

Are the two approaches the same?

identical(diamonds_middle, diamonds_middle_v2)

[1] TRUE

Better quality diamonds are typically cheaper?!

• Let’s clean up the tibble to only view the middle 95% of values for x, y, z

ggplot(diamonds_middle, aes(x, price)) + geom_point() + theme(axis.title = element_text(size=40), axis.text = element_text(size=32))
ggplot(diamonds_middle, aes(y, price)) + geom_point() + theme(axis.title = element_text(size=40), axis.text = element_text(size=32))
ggplot(diamonds_middle, aes(z, price)) + geom_point() + theme(axis.title = element_text(size=40), axis.text = element_text(size=32))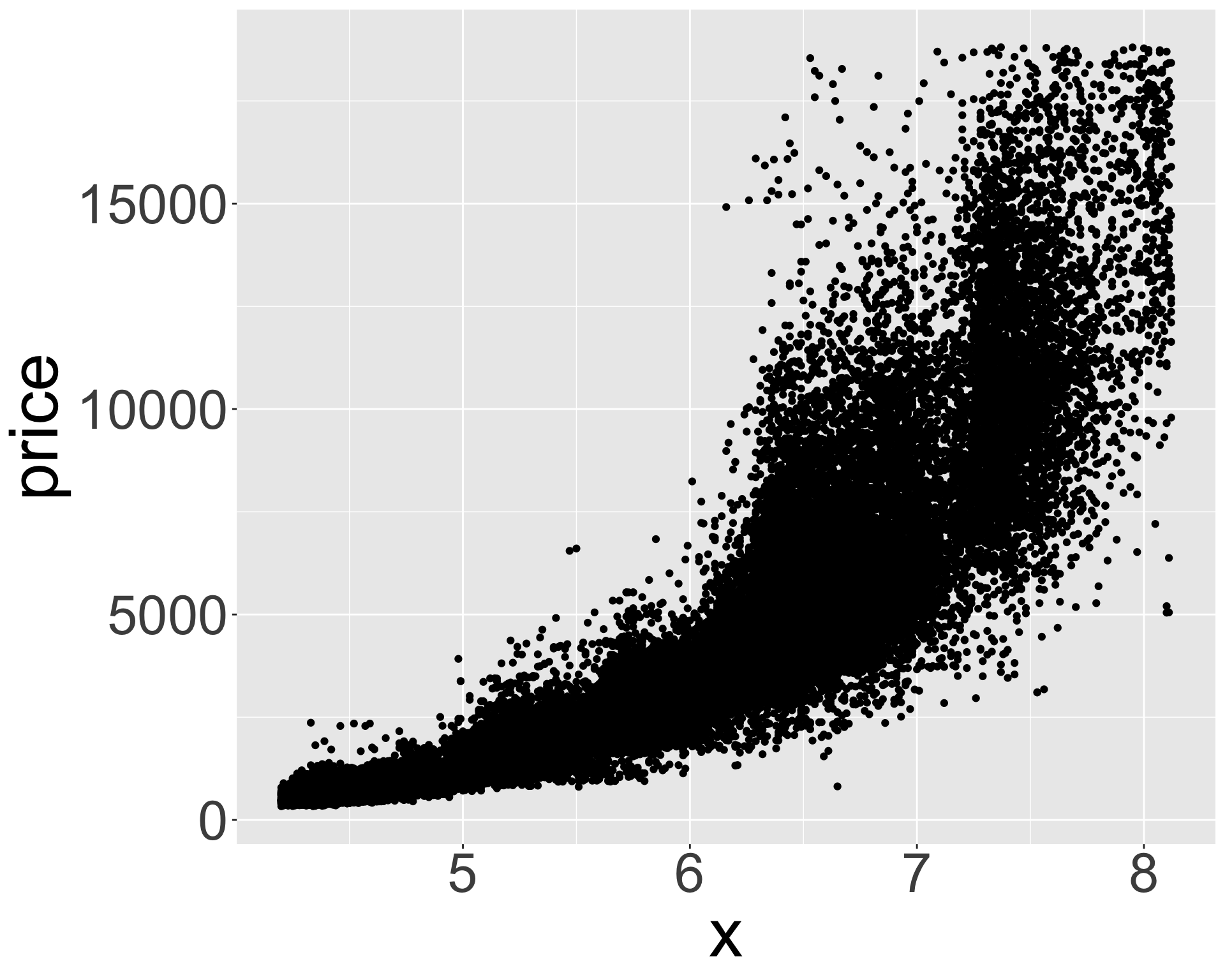

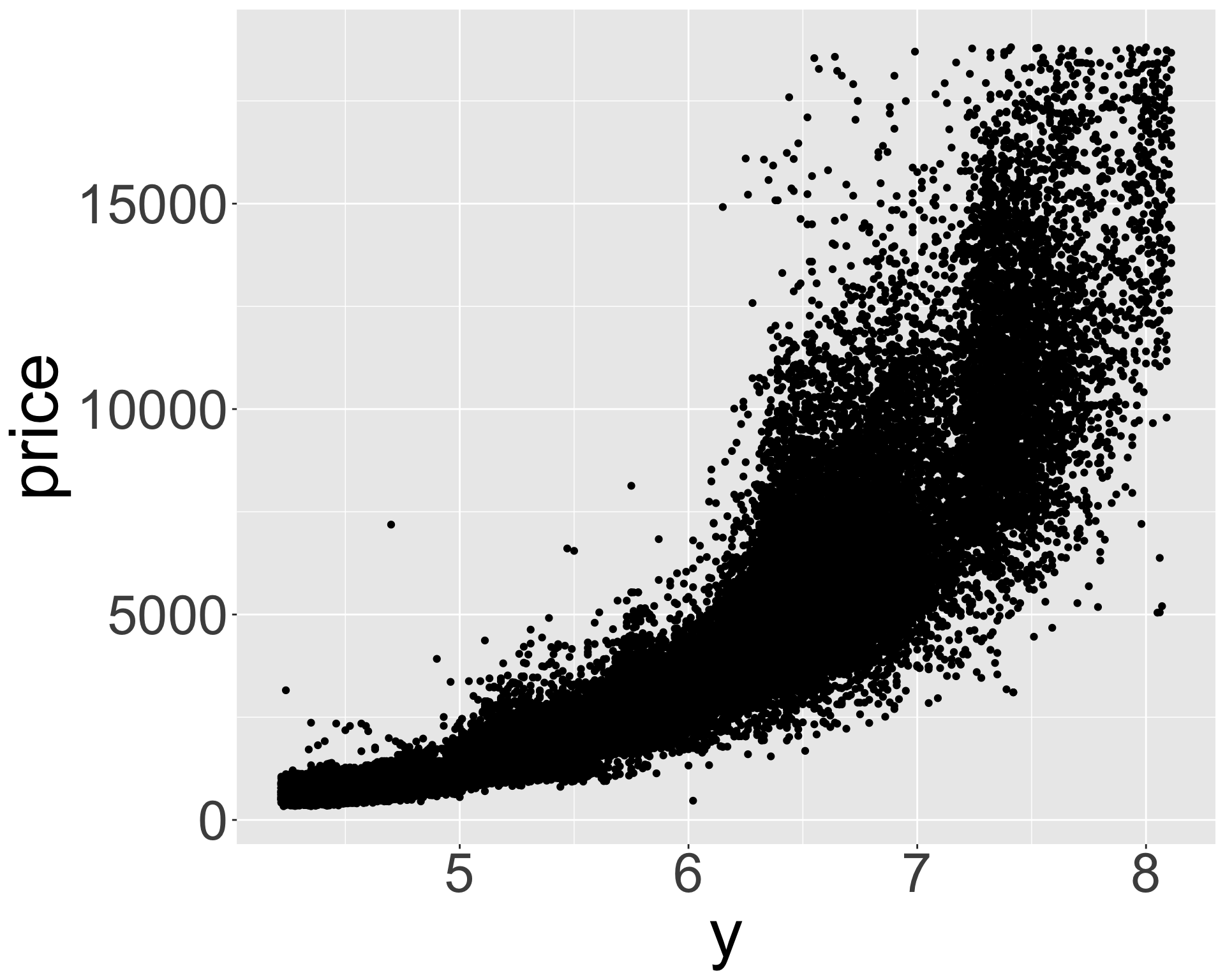
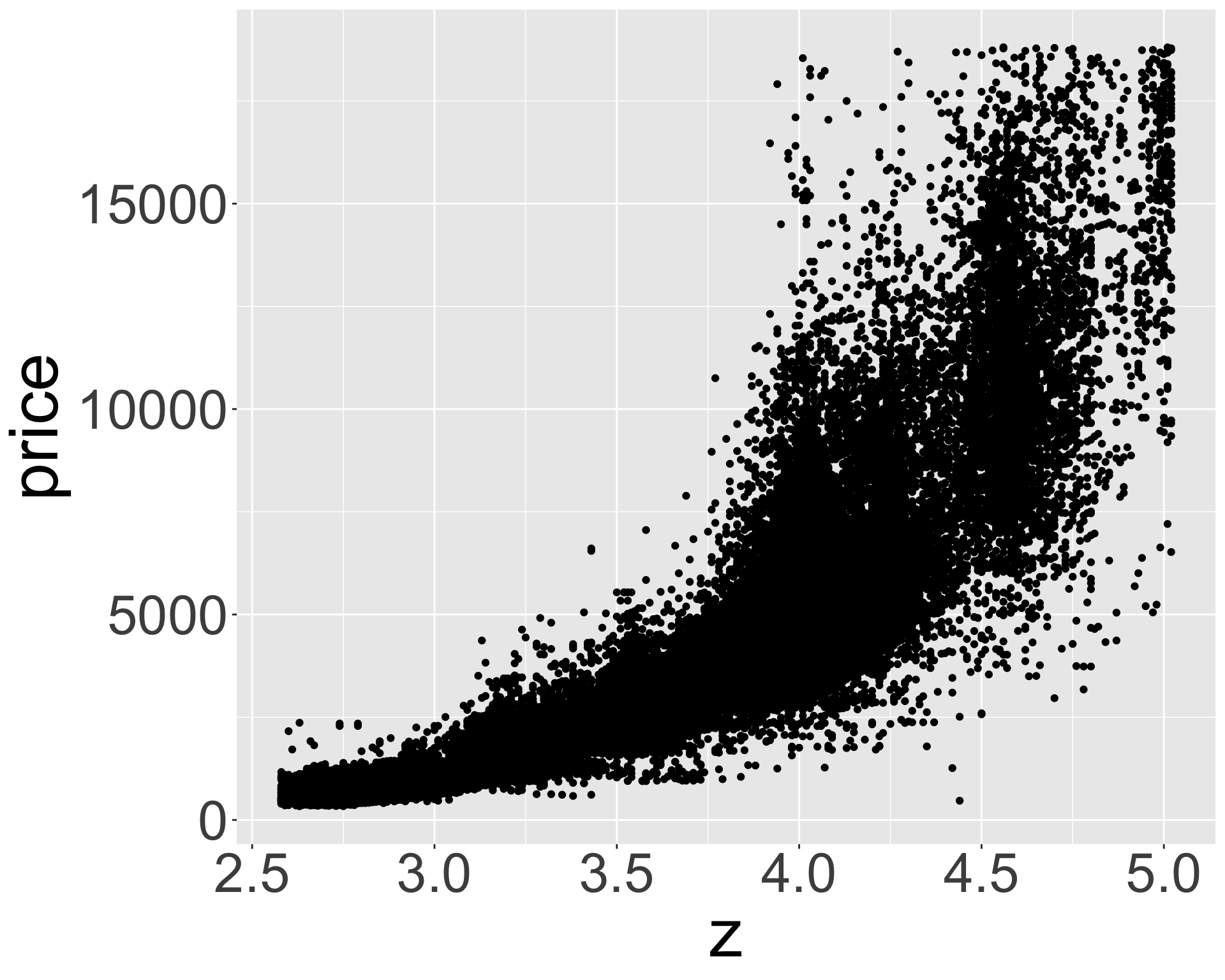
• Appears x, y, z (length/width/depth) are highly correlated with price
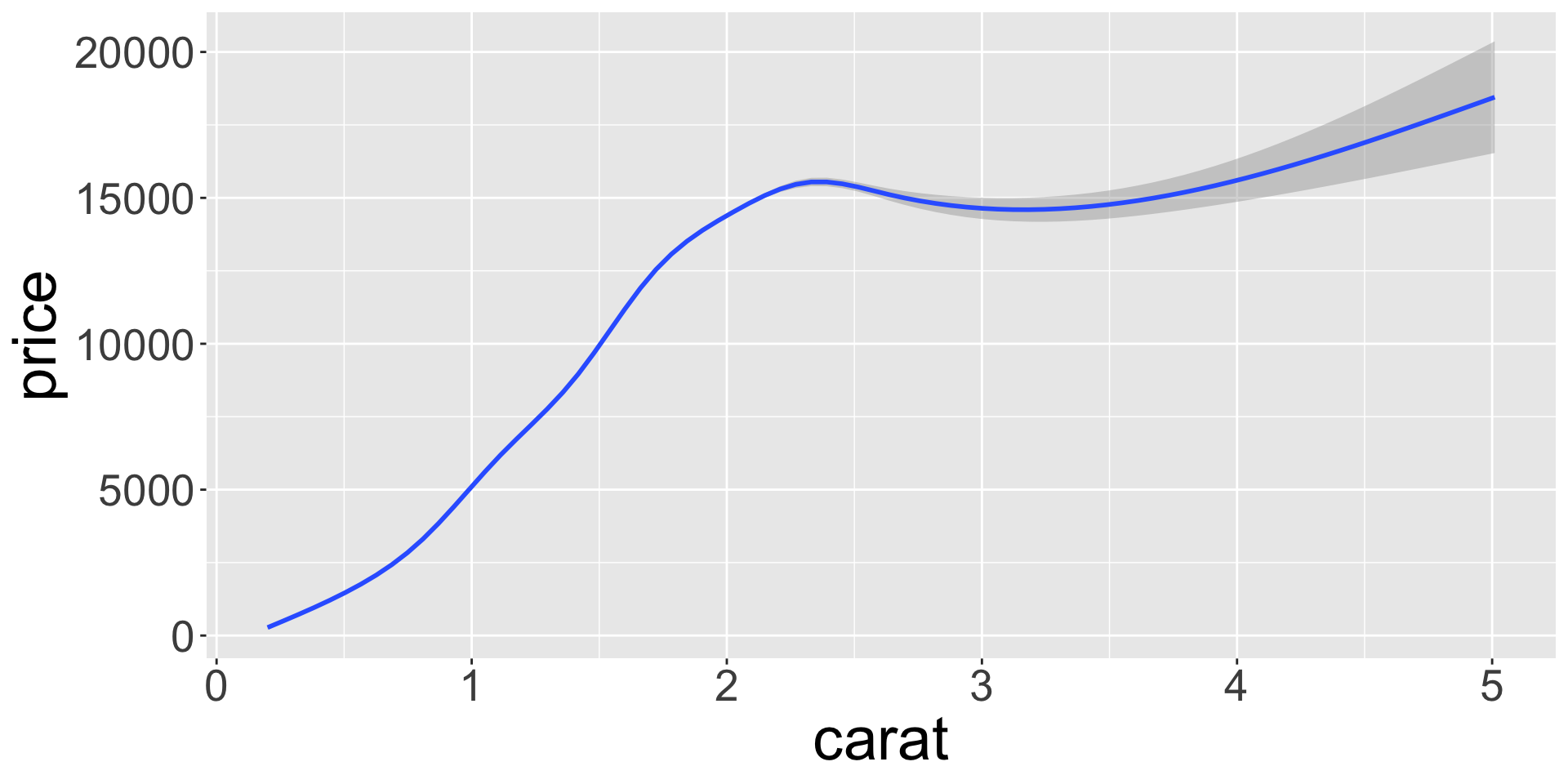
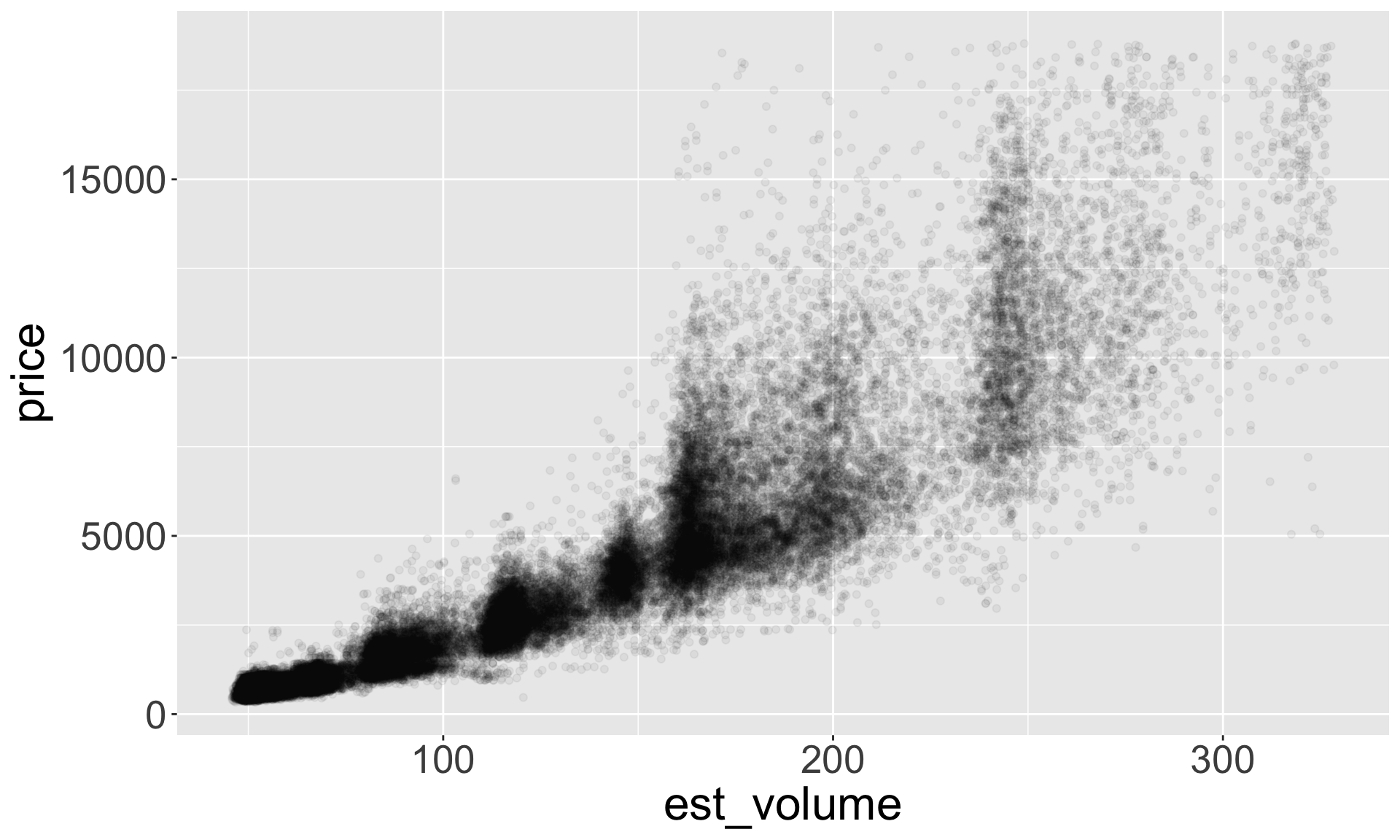
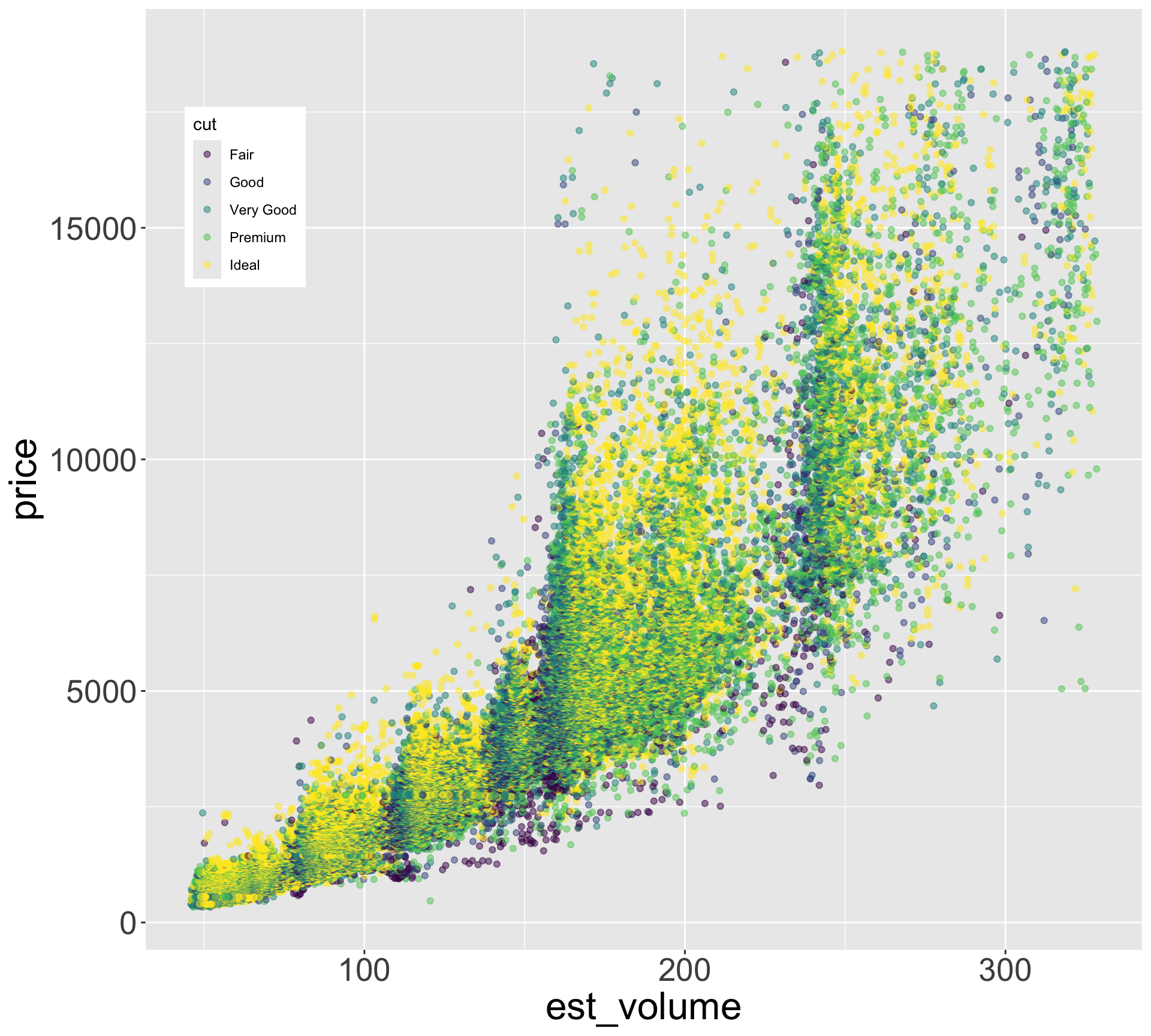
• Let’s explore the relationship between estimated volume (x*y*z) and price

Better quality diamonds are typically cheaper?!

• Let’s look at the relationship between estimated volume (x*y*z) and price

diamonds_middle |> 
  mutate(est_volume = x*y*z) |> 
  ggplot(aes(x = est_volume, y = price)) +
  geom_point(alpha = 0.05)

• Appears to be a strong correlation.
• Think about why we previously found that higher quality diamonds were cheaper.

Better quality diamonds are typically cheaper?!

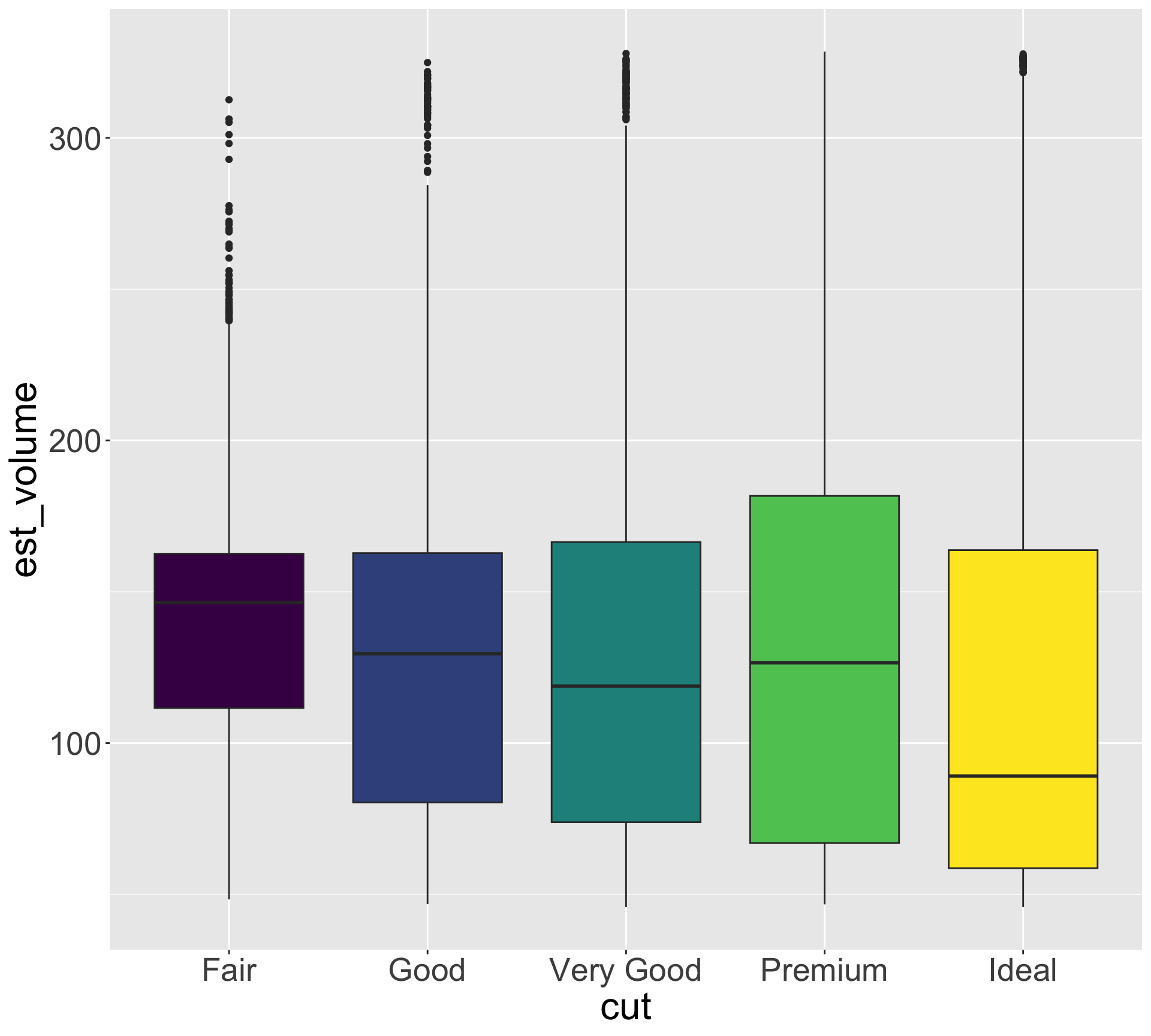
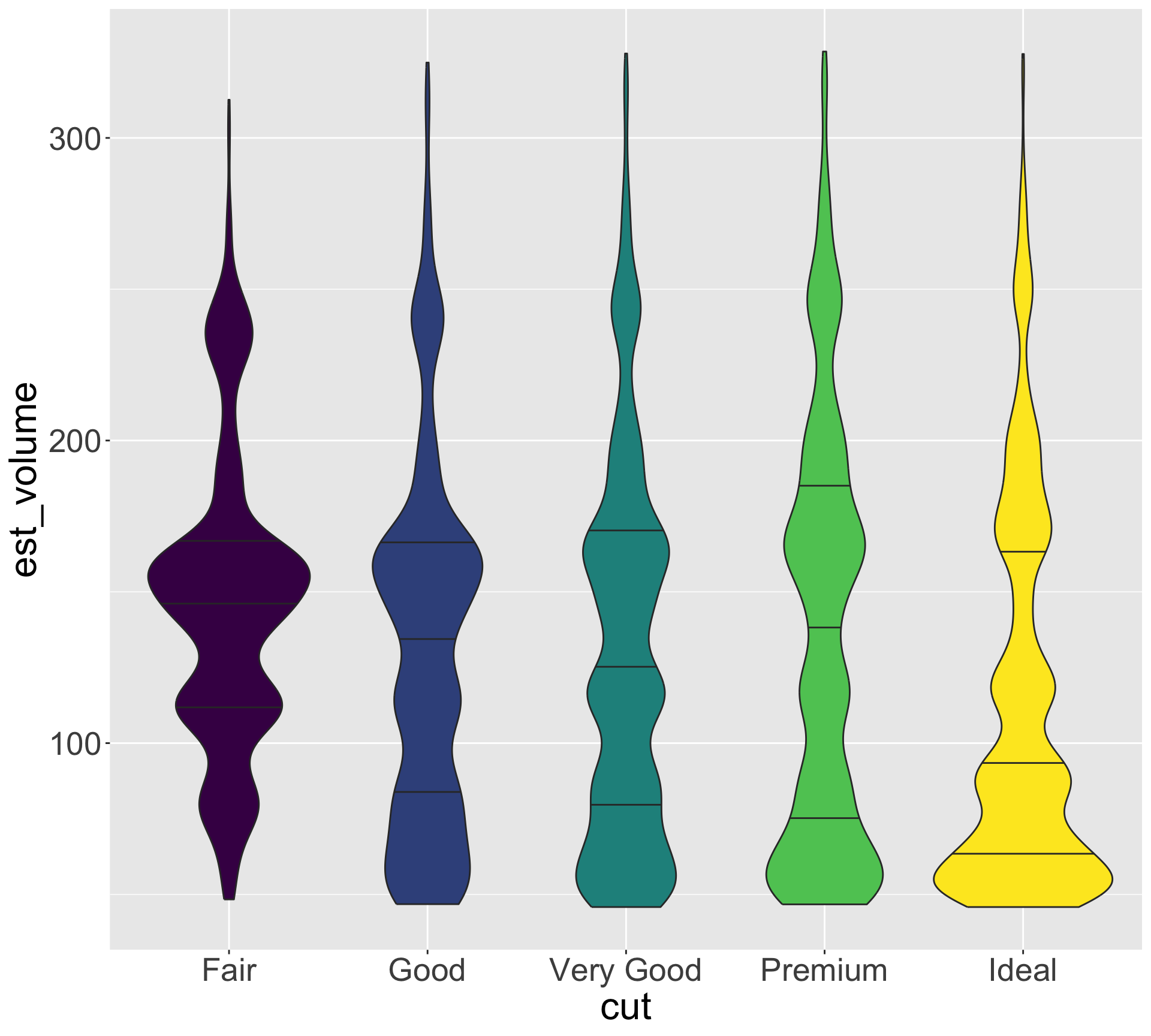
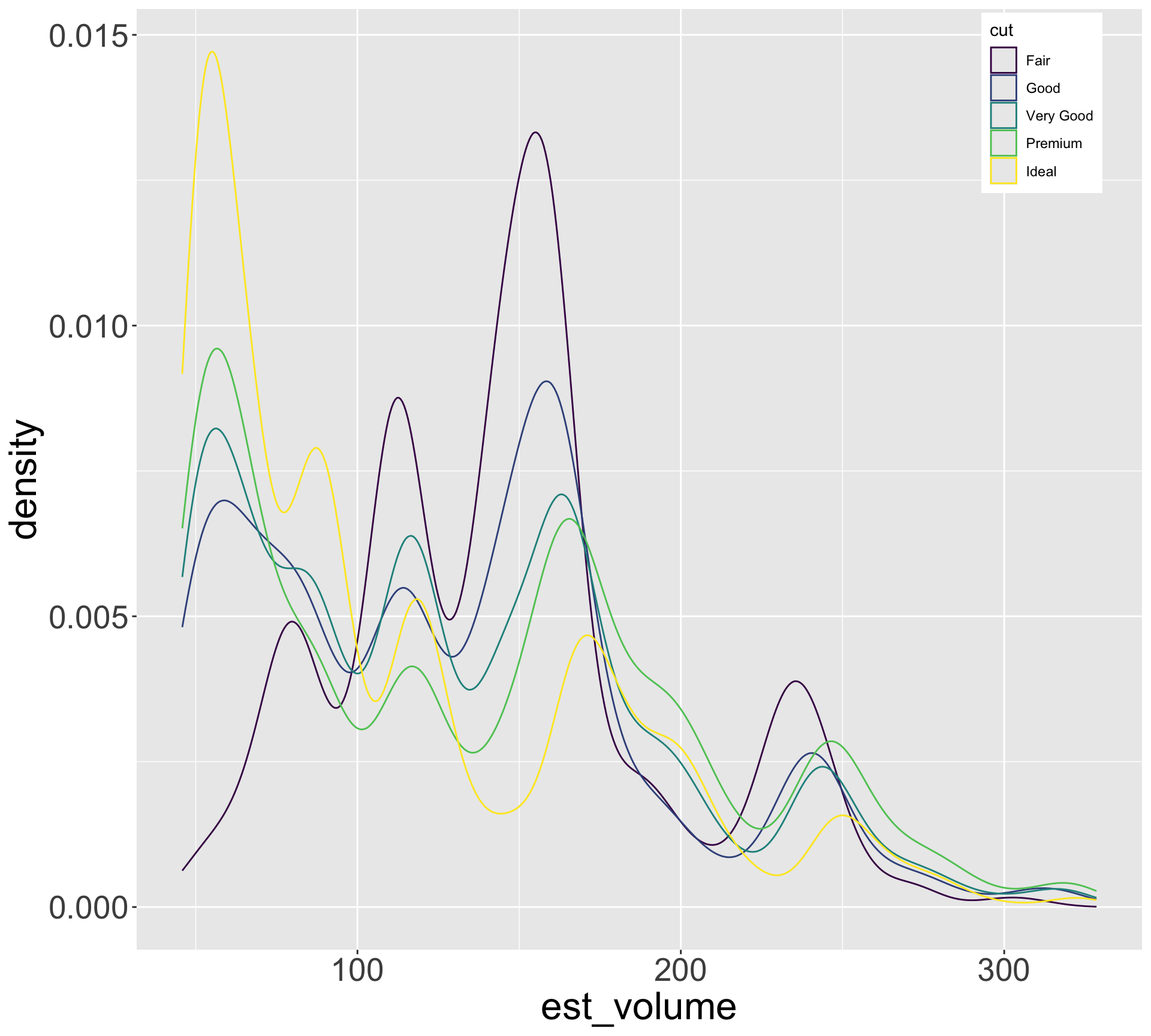
Hypothesis: high quality diamonds are smaller, low quality diamonds are larger.

• To investigate, let’s visualize variation in size for each category of quality

diamonds_middle |> 
  mutate(est_volume = x*y*z) |> 
  ggplot(aes(cut, est_volume, fill=cut)) +
  geom_boxplot() + 
  theme(legend.position="none")

diamonds_middle |> 
  mutate(est_volume = x*y*z) |> 
  ggplot(aes(cut, est_volume, fill=cut)) +
  geom_violin(draw_quantiles = c(0.25, 0.5, 0.75)) + 
  theme(legend.position="none")

diamonds_middle |> 
  mutate(est_volume = x*y*z) |> 
  ggplot(aes(est_volume, color=cut)) +
  geom_density() +
  theme(legend.position = c(0.9, 0.9))

Hypothesis seems reasonable

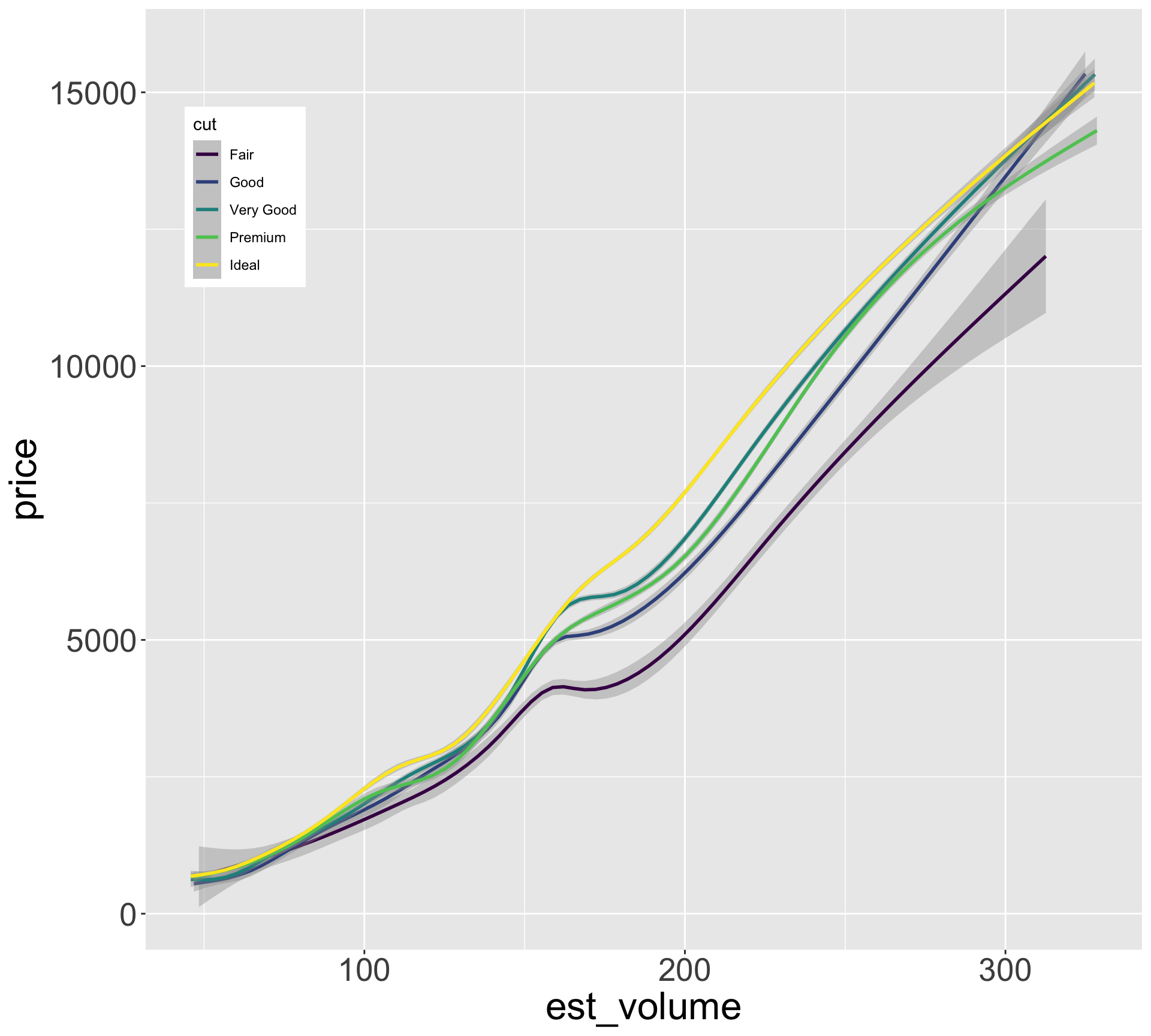
Better quality diamonds are typically cheaper?!

Now let’s look at size vs price for each cut

diamonds_middle |>
  mutate(est_volume = x*y*z) |>
  ggplot(aes(est_volume, price, color = cut)) +
  geom_point(alpha = 0.5) + 
  theme(legend.position = c(0.1, 0.8))

diamonds_middle |>
  mutate(est_volume = x*y*z) |>
  ggplot(aes(est_volume, price, color = cut)) +
  geom_smooth() + 
  theme(legend.position = c(0.1, 0.8))

Communicating ideas

Communicating ideas

• Now we’ll look at how to best display data once we’ve figured out some meaningful relationships between things
• Packages we’ll be using: tidyverse, scales, ggrepel, patchwork

Communicating ideas

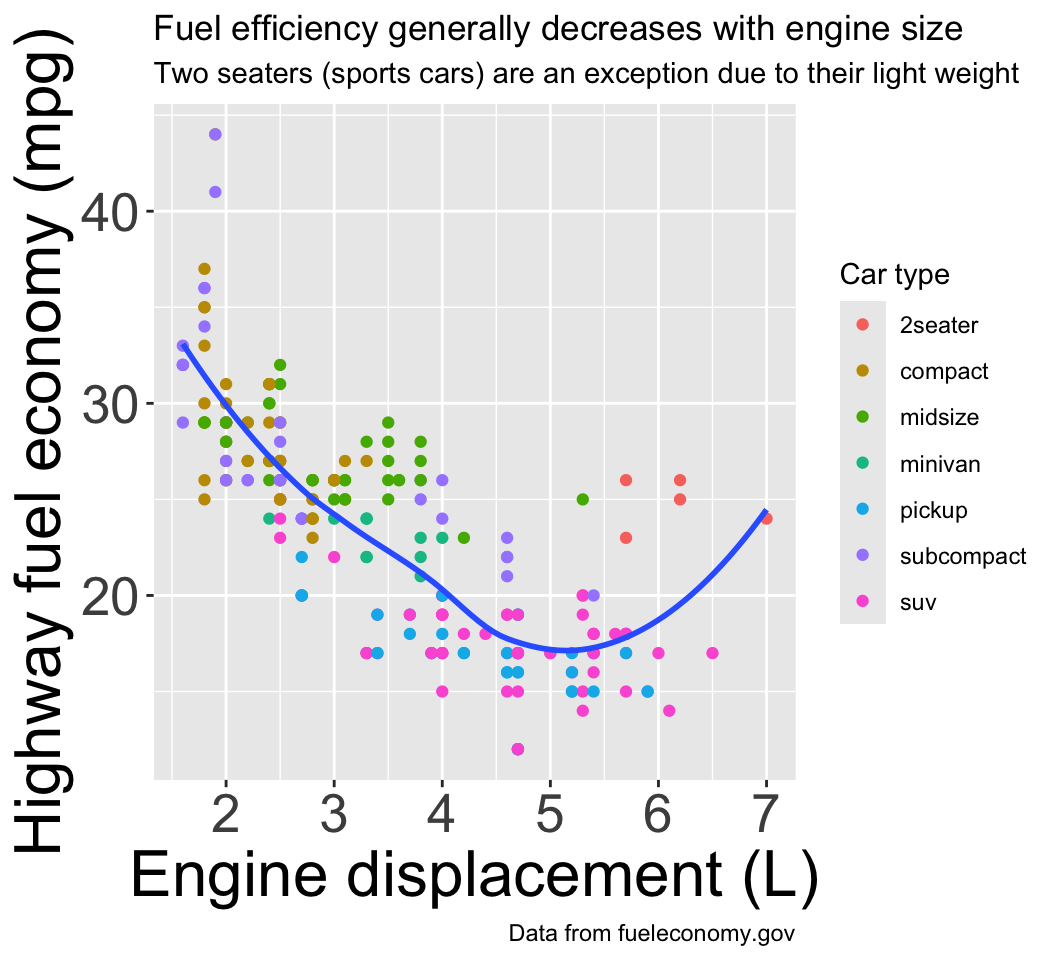
Good labels are crucial to good figures:

ggplot(mpg, aes(displ, hwy)) +
  geom_point(aes(color = class)) +
  geom_smooth(se = FALSE) +
  labs(
    x = "Engine displacement (L)",
    y = "Highway fuel economy (mpg)",
    color = "Car type",
    title = "Fuel efficiency generally decreases with engine size",
    subtitle = "Two seaters (sports cars) are an exception due to their light weight",
    caption = "Data from fueleconomy.gov"
  )

Annotations

pp <- mpg |> 
  ggplot(aes(displ, hwy, color = drv)) + 
  geom_point(alpha = 0.3) + 
  geom_smooth(se = FALSE) +
  theme(legend.position = c(0.9, 0.8)) +
  labs(x = "Engine displacement (L)", y = "Highway fuel economy (mpg)", color = "Drive train", title = "Fuel efficiency generally decreases with engine size")

pp

How can we improve this plot? (What is 4, f, r?)

Annotations

Often helpful to label individual observations or groups of observations

• geom_text(), similar to geom_point() but has additional aesthetic label.
• Label could come from tibble itself, or could use custom user-added labels

• Let’s create custom labels

label_info <- mpg |>
  group_by(drv) |>
  arrange(desc(displ)) |>
  slice_head(n = 1) |>
  mutate(
    drive_type = case_when(
      drv == "f" ~ "front-wheel drive",
      drv == "r" ~ "rear-wheel drive",
      drv == "4" ~ "4-wheel drive"
    )
  ) |>
  select(displ, hwy, drv, drive_type)

label_info

# A tibble: 3 × 4
# Groups:   drv [3]
  displ   hwy drv   drive_type       
  <dbl> <int> <chr> <chr>            
1   6.5    17 4     4-wheel drive    
2   5.3    25 f     front-wheel drive
3   7      24 r     rear-wheel drive 

• Can use label_info to directly label groups and replace legend
• x and y aesthetics the same as in the original mpg tibble

Annotations

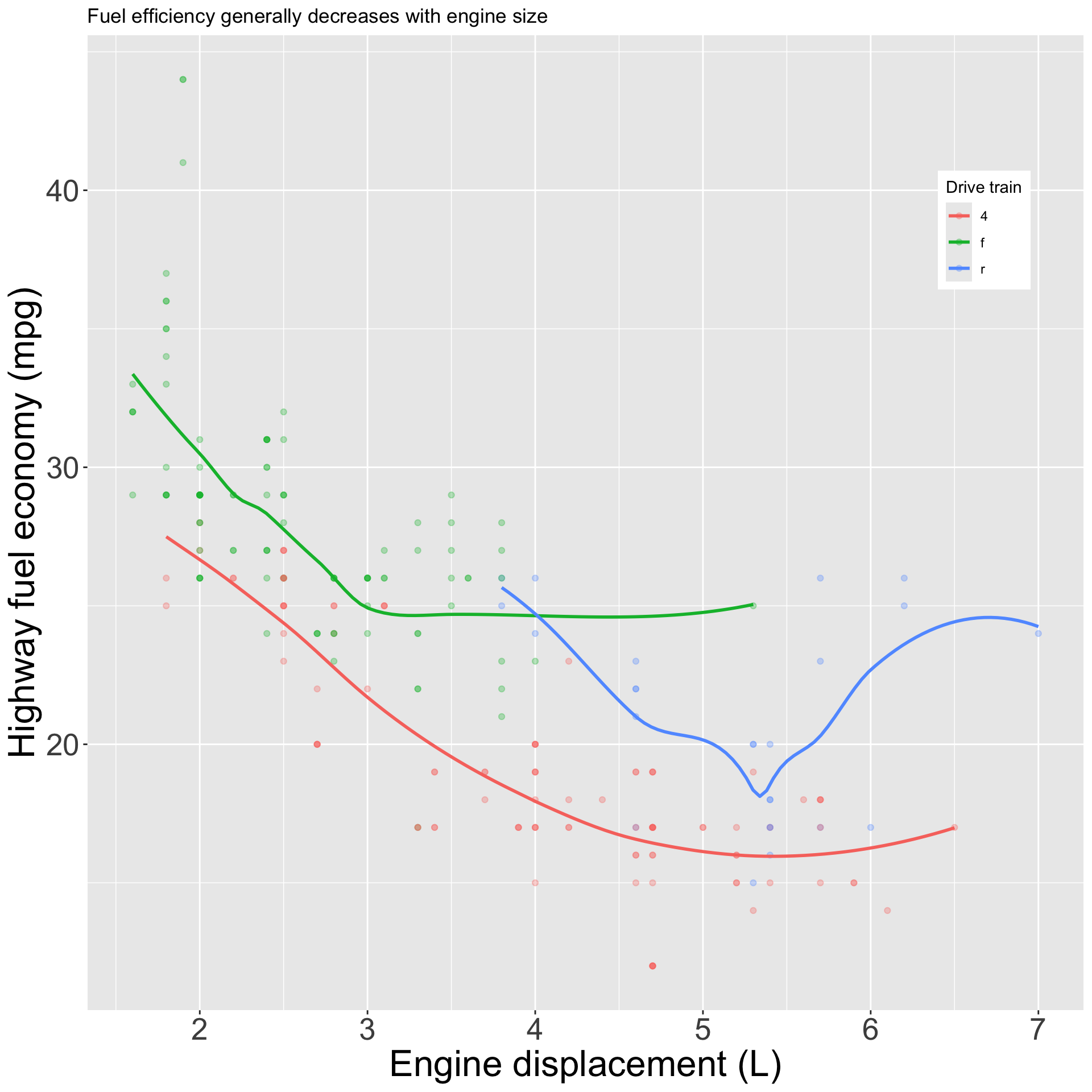
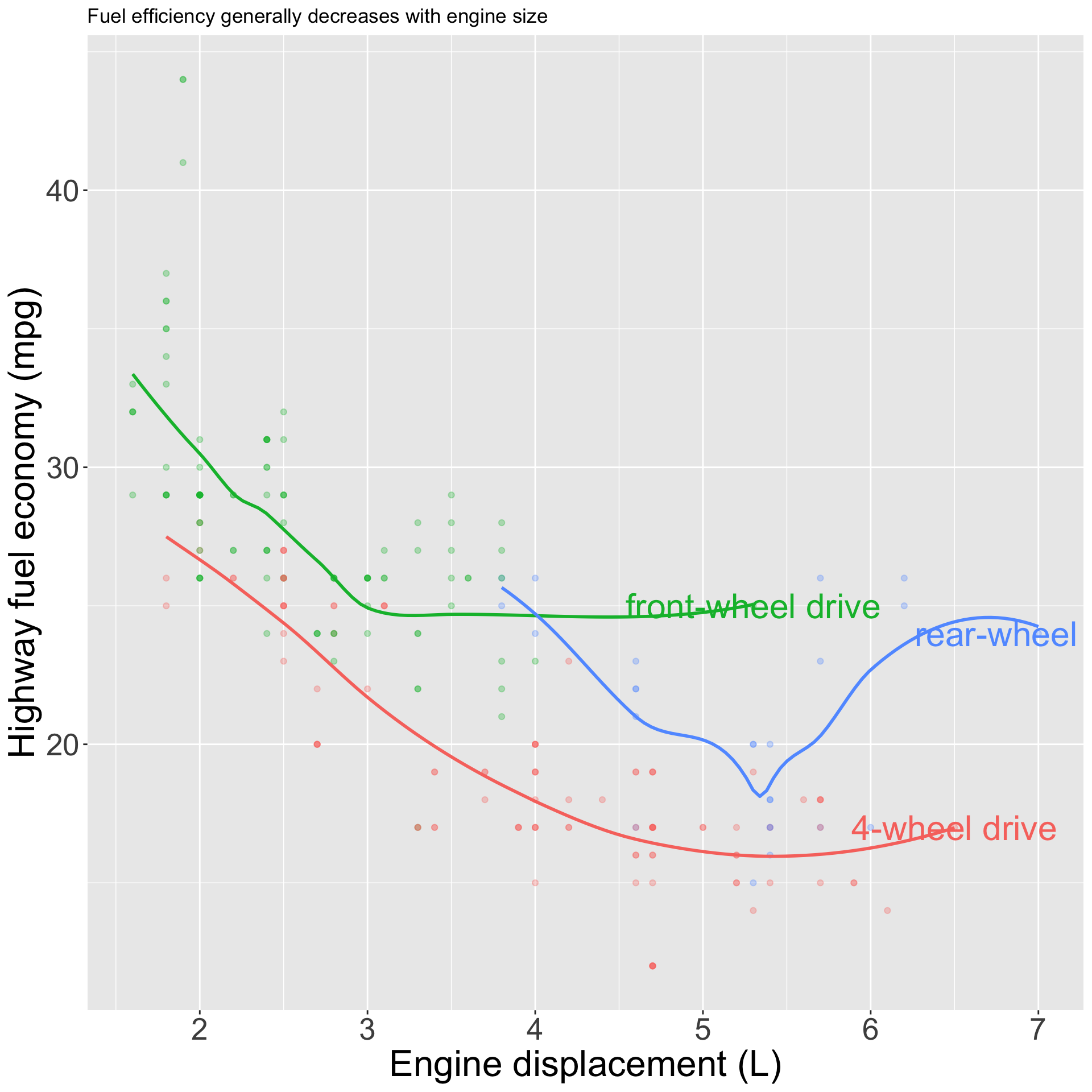
pp <- mpg |> 
  ggplot(aes(displ, hwy, color = drv)) + 
  geom_point(alpha = 0.3) + 
  geom_smooth(se = FALSE) +
  geom_text(
    data = label_info,
    aes(label = drive_type),
    size = 8
  ) +
  theme(legend.position = "none") +
  labs(x = "Engine displacement (L)", y = "Highway fuel economy (mpg)", color = "Drive train", title = "Fuel efficiency generally decreases with engine size")

pp

Annotations

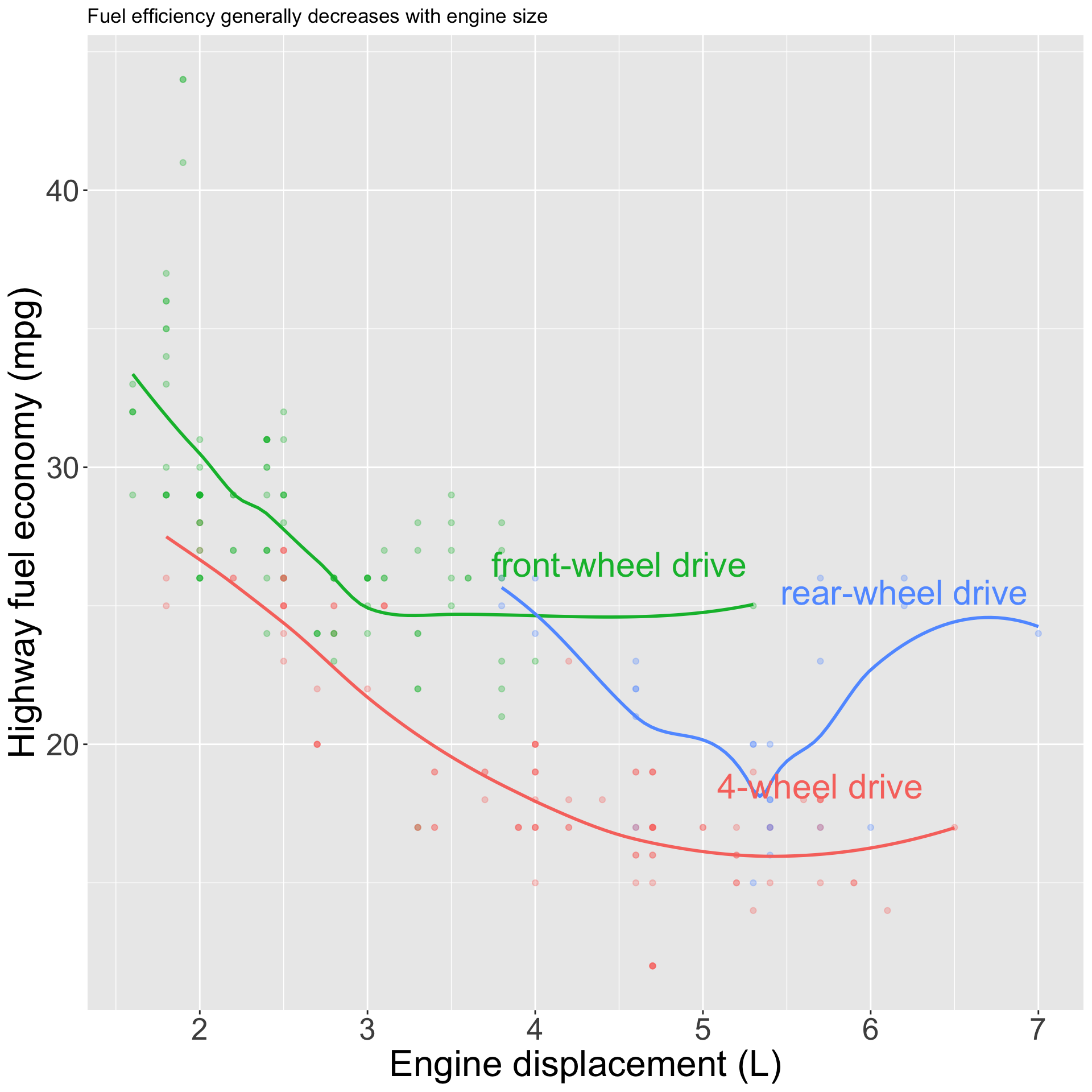
pp <- mpg |> 
  ggplot(aes(displ, hwy, color = drv)) + 
  geom_point(alpha = 0.3) + 
  geom_smooth(se = FALSE) +
  geom_text(
    data = label_info,
    aes(label = drive_type),
    nudge_y = 1.5, nudge_x = -0.8, 
    size = 8
  ) +
  theme(legend.position = "none") +
  labs(x = "Engine displacement (L)", y = "Highway fuel economy (mpg)", color = "Drive train", title = "Fuel efficiency generally decreases with engine size")

pp

Annotations

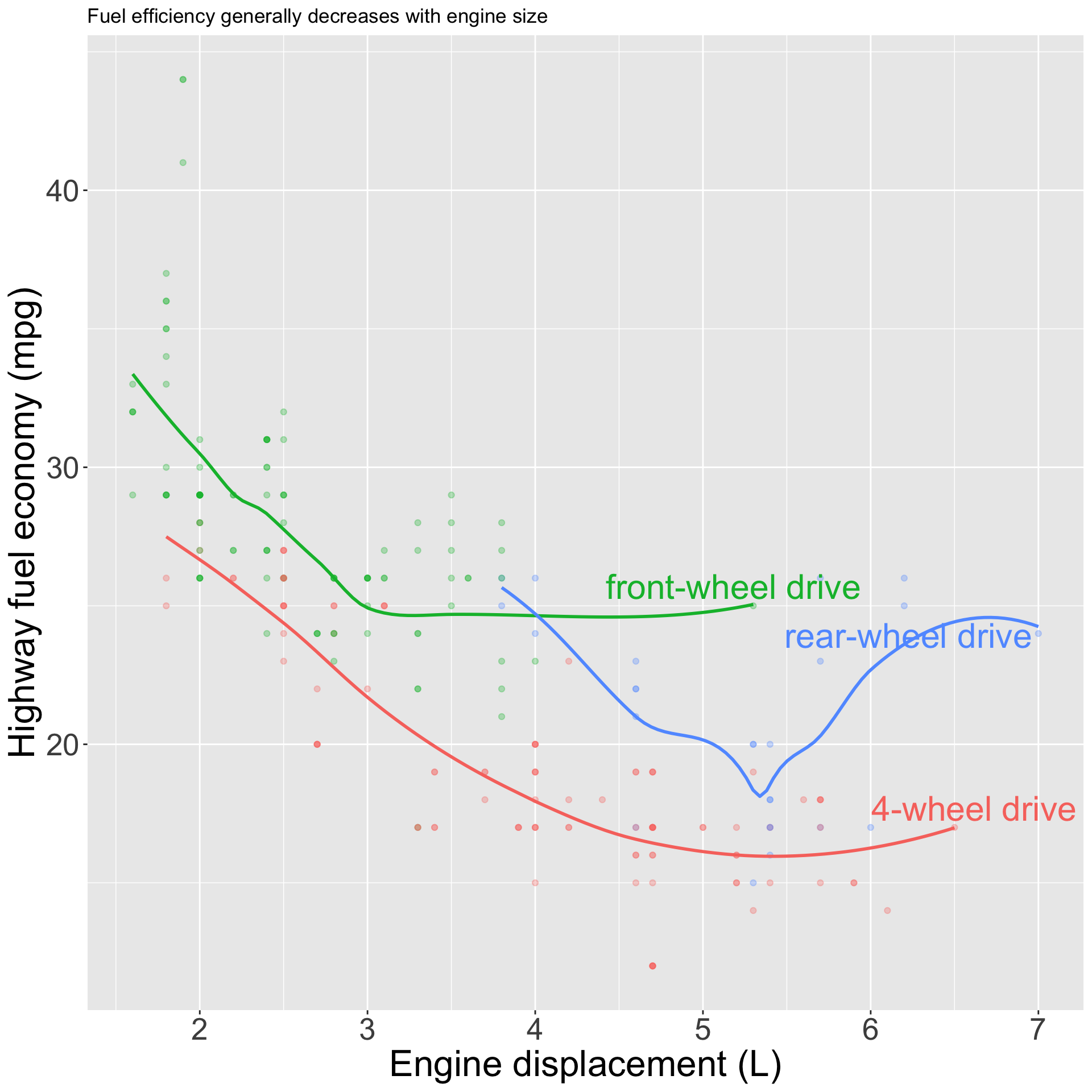
pp <- mpg |> 
  ggplot(aes(displ, hwy, color = drv)) + 
  geom_point(alpha = 0.3) + 
  geom_smooth(se = FALSE) +
  geom_text_repel(
    data = label_info,
    aes(label = drive_type),
    size = 8
  ) +
  theme(legend.position = "none") +
  labs(x = "Engine displacement (L)", y = "Highway fuel economy (mpg)", color = "Drive train", title = "Fuel efficiency generally decreases with engine size")

pp

Annotations

Same idea can be used to highlight points on plot, e.g. outliers

potential_outliers <- mpg |> filter(hwy > 40 | (hwy > 20 & displ > 5))
ggplot(mpg, aes(displ, hwy)) +
  geom_point() +
  geom_text_repel(data = potential_outliers, aes(label = model)) +
  geom_point(data = potential_outliers, shape = "circle open", color = "red", size = 3) + 
  labs(x = "Engine displacement (L)", y = "Highway fuel economy (mpg)", color = "Drive train", title = "Fuel efficiency generally decreases with engine size")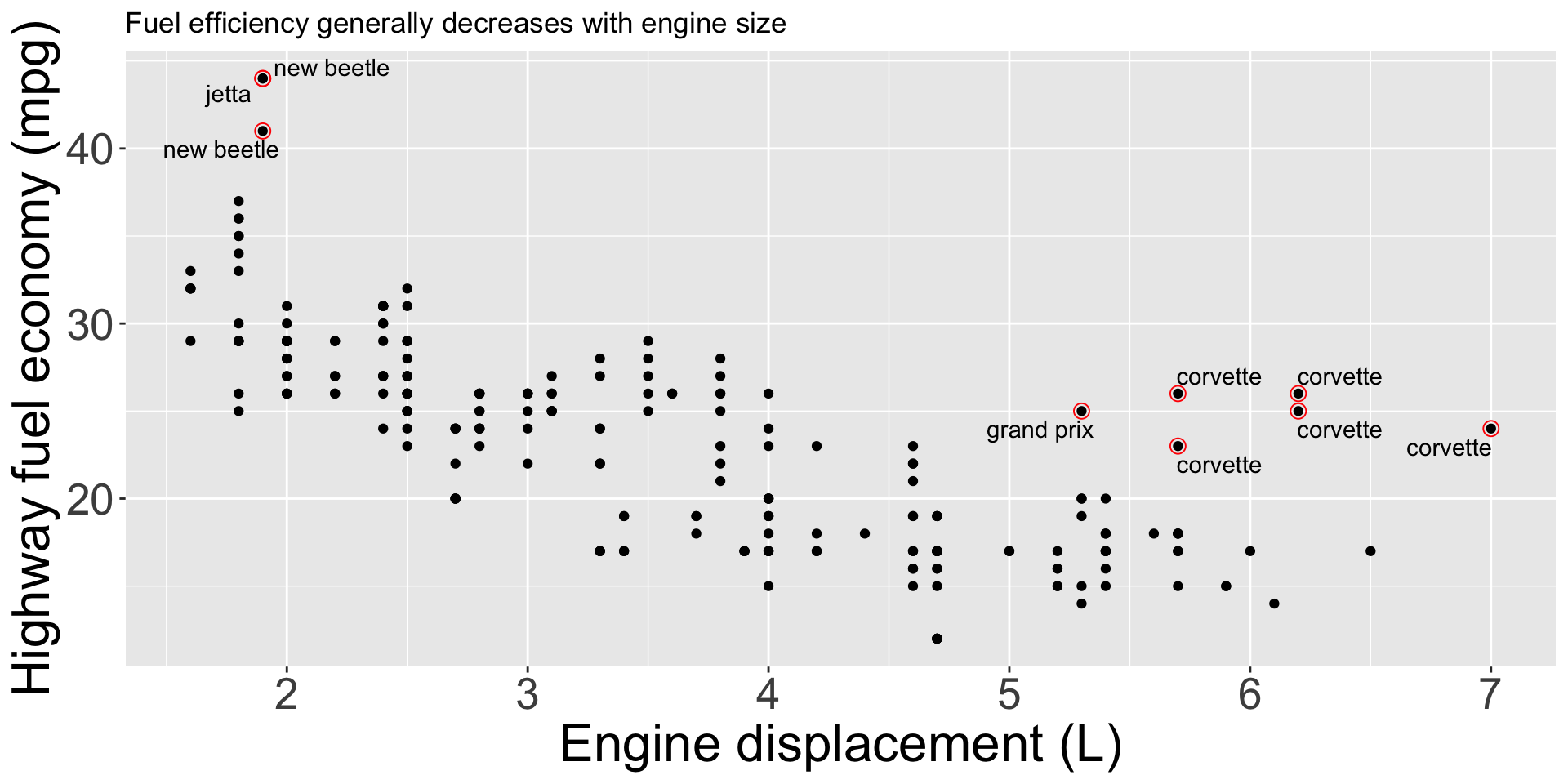

Annotations

• Other annotations which you might encounter / could be useful:
  • geom_hline(), geom_vline(): create horizontal / vertical lines
  • geom_rect(): rectangle around points of interest, require specifying xmin, xmax, ymin, ymax
  • geom_segment(): draw an arrow from one point to another
• Function which allows for doing any of these: annotate()
• Let’s say we want to add some text to our plot, but split lines every 30 characters using str_wrap()

trend_text <- "Larger engine sizes tend to have lower fuel economy." |>
  str_wrap(width = 30)
trend_text

[1] "Larger engine sizes tend to\nhave lower fuel economy."

Annotations

• Let’s add a text label in red using annotate(geom = 'label')
• … and then add a line segment giving general trend

ggplot(mpg, aes(displ, hwy)) +
  geom_point() +
  annotate(
    geom = "label", x = 3.5, y = 38,
    label = trend_text,
    hjust = "left", color = "red"
  ) +
  annotate(
    geom = "segment", x = 3, y = 35, 
    xend = 5, yend = 25, color = "red",
    arrow = arrow(type = "closed")
  )

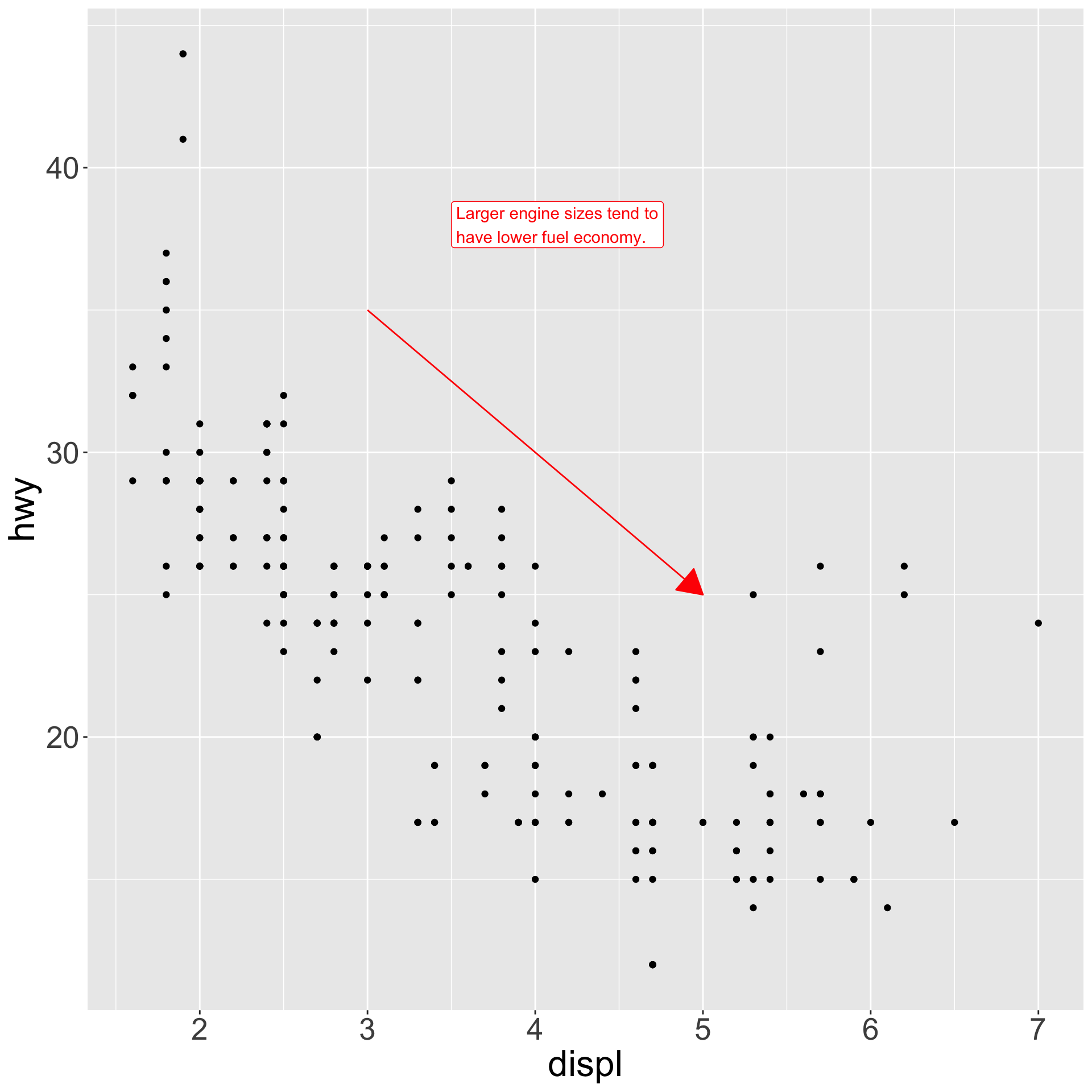
Axis ticks

Axes and legends are called guides in R.

• Axes used for x,y aesthetics, legends for everything else
• Ticks on axes and keys on legend affected by args breaks and labels.

ggplot(mpg, aes(displ, hwy, color = drv)) +
  geom_point() +
  scale_y_continuous(breaks = seq(15, 40, by = 5))

ggplot(mpg, aes(displ, hwy, color = drv)) +
  geom_point() +
  scale_x_continuous(labels = NULL) +
  scale_y_continuous(labels = NULL) +
  scale_color_discrete(labels = c("4" = "4-wheel", "f" = "front", "r" = "rear"))

Axis ticks

• Specifying labels and breaks provides a lot of flexibility on how to plot

ggplot(diamonds, aes(price, cut, fill = cut)) +
  geom_boxplot(alpha = 0.1) +
  scale_x_continuous(labels = label_dollar()) + 
  theme(legend.position = "none")

ggplot(diamonds, aes(price, cut, fill = cut)) +
  geom_boxplot(alpha = 0.1) +
  scale_x_continuous(
    labels = label_dollar(scale = 1/1000, suffix = "K"),
    breaks = seq(1000, 19000, by = 4000) 
  ) + 
  theme(legend.position = "none")

Legends

To control location of legend, use theme() (controls non data parts of a plot)

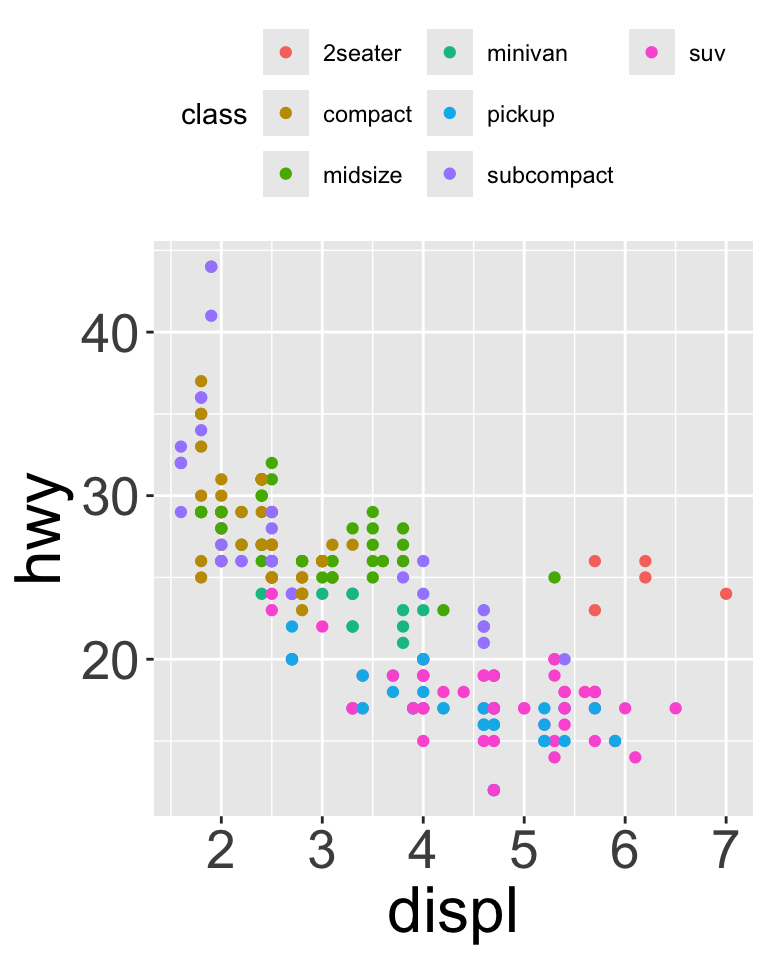
base <- ggplot(mpg, aes(x = displ, y = hwy)) + geom_point(aes(color = class))

base + theme(legend.position = "right")  # the default
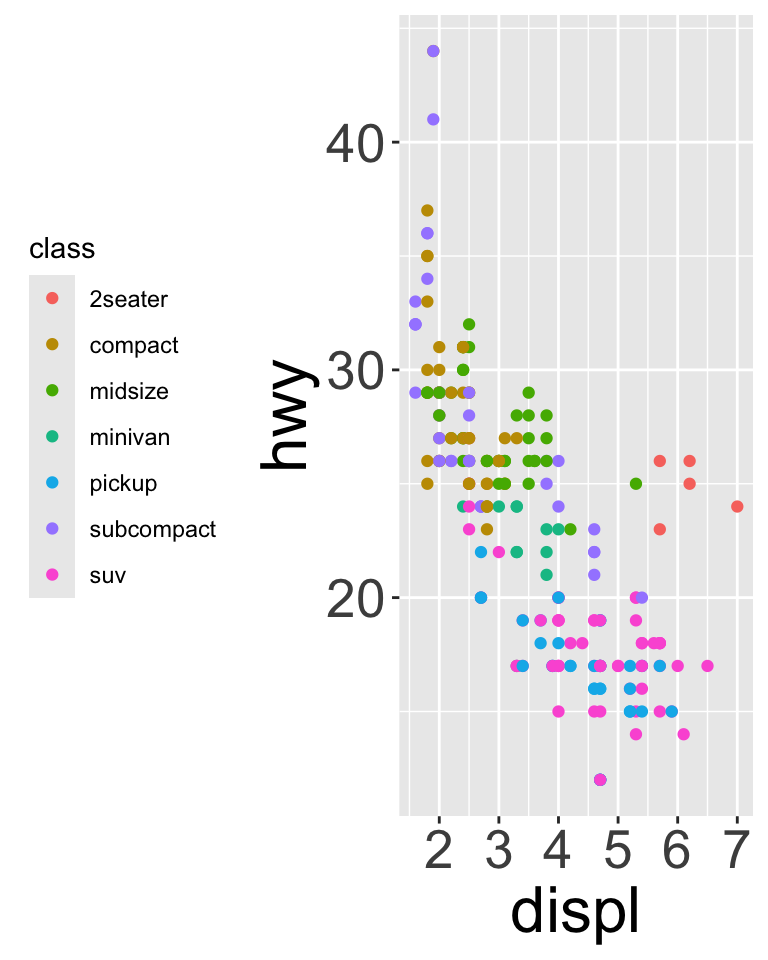
base + theme(legend.position = "left")
base + theme(legend.position = "top") + guides(color = guide_legend(nrow = 3))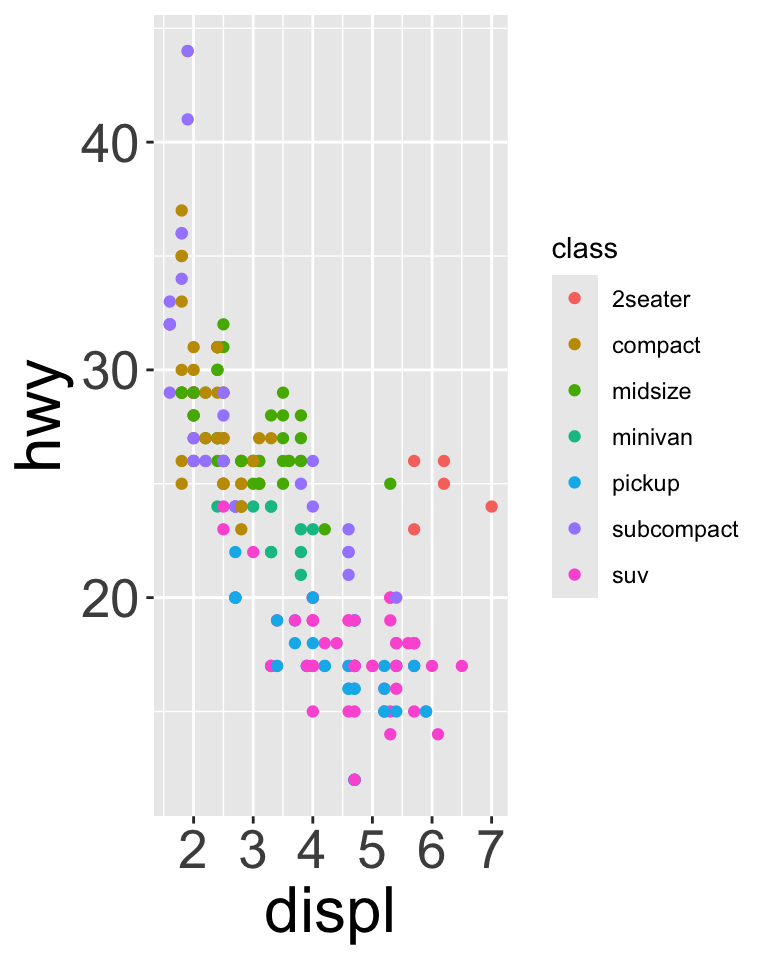

Replacing scales

• Often useful to transform data, e.g. log transformations

diamonds |> 
  ggplot(aes(carat, price)) +
  geom_point(alpha = 0.02)
diamonds |> 
  ggplot(aes(log10(carat), log10(price))) +
  geom_point(alpha = 0.02)

• A useful geom for large-sample-size datasets: geom_bin2d()

# Left
ggplot(diamonds, aes(carat, price)) +
  geom_bin2d()
# Right
ggplot(diamonds, aes(log10(carat), log10(price))) +
  geom_bin2d()

Replacing scales

• Can use scale_x_log10() and scale_y_log190) to plot regular values, but with ticks that are spread using a log scale

ggplot(diamonds, aes(carat, price)) +
  geom_bin2d()

ggplot(diamonds, aes(carat, price)) +
  geom_bin2d() +
  scale_x_log10() + scale_y_log10()

Replacing scales

• Color scales are also often replaced; especially using scale_color_brewer()

ggplot(mpg, aes(displ, hwy)) +
  geom_point(aes(color = drv))

ggplot(mpg, aes(displ, hwy)) +
  geom_point(aes(color = drv)) +
  scale_color_brewer(palette = "Set1")

Replacing scales

Many options for color brewer

RColorBrewer::display.brewer.all()

• One group goes from light to dark colors.
• Another group is a set of non ordinal colors.
• Last group has diverging scales (from dark to light to dark again).

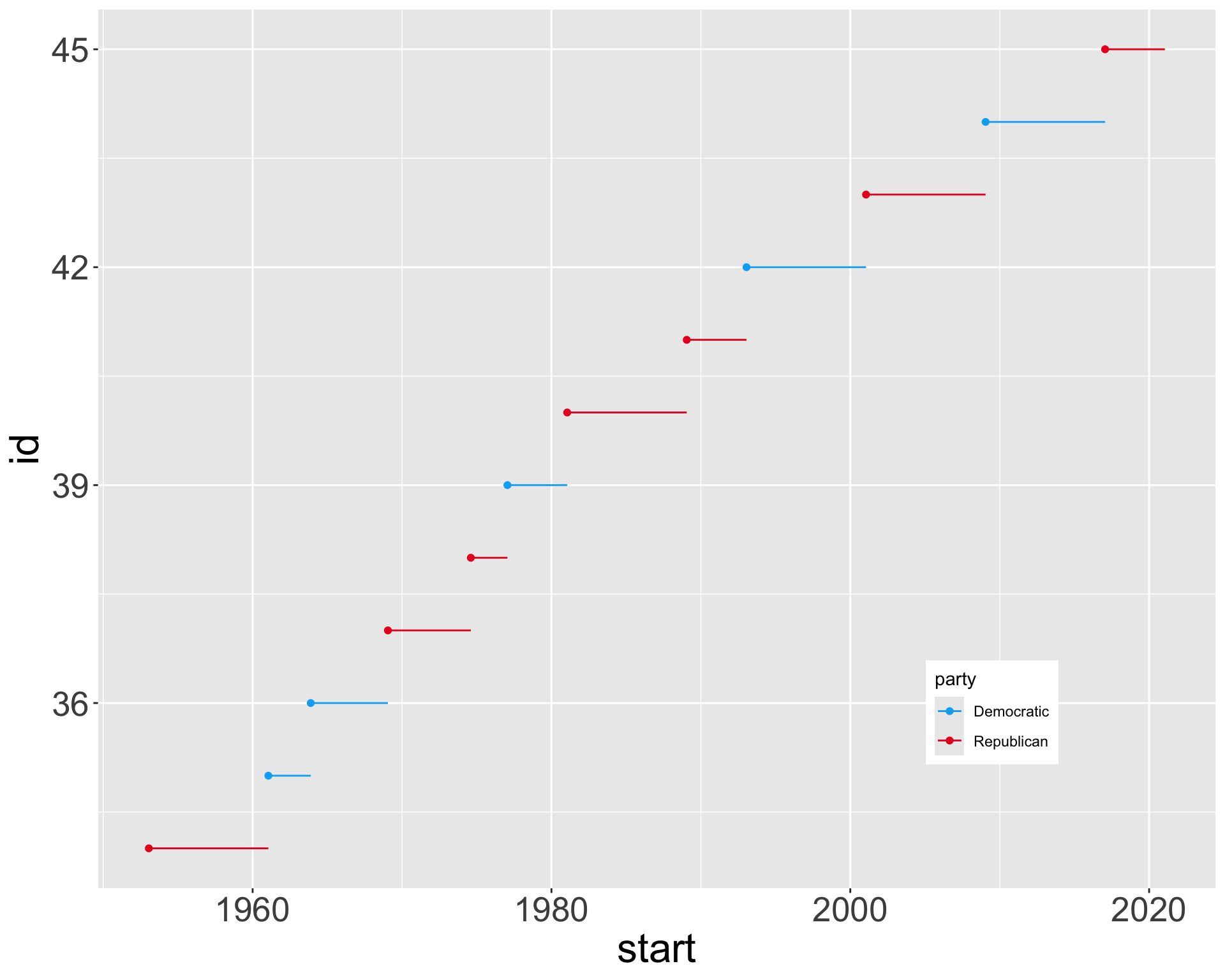
Manual color scaling

scale_color_manual() allows giving specific colors for groups in the tibble

presidential |> head()

# A tibble: 6 × 4
  name       start      end        party     
  <chr>      <date>     <date>     <chr>     
1 Eisenhower 1953-01-20 1961-01-20 Republican
2 Kennedy    1961-01-20 1963-11-22 Democratic
3 Johnson    1963-11-22 1969-01-20 Democratic
4 Nixon      1969-01-20 1974-08-09 Republican
5 Ford       1974-08-09 1977-01-20 Republican
6 Carter     1977-01-20 1981-01-20 Democratic

• Takes argument values: a named vector, with entries of the form group=color.
• color can be either English names (“blue”, “red”) or hexadecimal color codes

presidential |>
  mutate(id = 33 + row_number()) |>
  ggplot(aes(start, id, color = party)) +
  geom_point() +
  geom_segment(aes(xend = end, yend = id)) +
  scale_color_manual(
    values = c(Republican = "#E81B23",
               Democratic = "#00AEF3")) + 
  theme(legend.position = c(0.8, 0.2))